Prosta

Ten artykuł dotyczy pojęcia geometrycznego. Zobacz też: wzniesienie Prosta w Sudetach.

Linia prosta lub prosta – jedno z podstawowych pojęć geometrii, szczególny przypadek nieograniczonej z obydwu stron krzywej o nieskończonym promieniu krzywizny w każdym punkcie^[1].

W niektórych ujęciach, w tym w klasycznej geometrii euklidesowej, prosta jest tzw. pojęciem pierwotnym^[2], niedefiniowanym formalnie w obrębie danej teorii. Można ją jednak interpretować za pomocą pojęć wykraczających poza geometrię, np. jako zbiór punktów o współrzędnych spełniających pewne równanie. Ten temat szerzej omówiony jest w artykule dotyczącym geometrii euklidesowej.

W matematyce rozważane są także inne geometrie, takie jak geometria powierzchni kuli^[3]. Pojęcie prostej można uogólnić także na tzw. geometrie nieeuklidesowe^[4]. Odpowiednikiem prostych są wówczas tzw. linie geodezyjne, czyli krzywe określające lokalnie najkrótsze drogi między punktami^[5]. Według najogólniejszej definicji zatem:

Prosta (geodezyjna) to nieposiadająca zakończeń krzywa o jednej gałęzi i zerowej krzywiźnie geodezyjnej w każdym punkcie (czyli zerowej pochodnej kowariantnej dla kierunku tej krzywej w każdym punkcie)^[6].

W pewnym więc sensie proste w dowolnych przestrzeniach nadal są liniami niezakrzywionymi.

Geometria euklidesowa

Linia prosta w sensie potocznym różni się od tego, co pod tym pojęciem określa się w matematyce. Potocznie „prosta” oznacza „niezakrzywiona”. W geometrii euklidesowej „prosta” albo „linia prosta”, oprócz tego, że nie jest zakrzywiona, musi rozciągać się nieograniczenie w obydwie strony i mieć zerową „grubość”.

Jeśli niezakrzywiona linia o zerowej grubości rozciąga się nieograniczenie tylko w jedną stronę, a z drugiej strony ma zakończenie, to jest nazywana „półprostą”. Jeśli posiada zakończenia z obydwu stron, to nazywana jest „odcinkiem”.

Definicja Euklidesa

 Zobacz też: Elementy i geometria euklidesowa.

Nazwa geometrii euklidesowej pochodzi od greckiego matematyka Euklidesa, który w III w. p.n.e. w swoim dziele Elementy po raz pierwszy zebrał i systematycznie udowodnił większość znanych podówczas twierdzeń geometrycznych.

Euklides w Elementach podał 23 definicje różnych pojęć geometrycznych w tym punktu, linii (krzywej), prostej, kąta. Prostą definiował tak:

• linia jest długością bez szerokości^[7],
• linia jest prosta, jeśli jest położona między swoimi punktami w równym i jednostajnym kierunku^[8].

Definicja ta z punktu widzenia dzisiejszej matematyki pasuje raczej do odcinka niż do prostej, gdyż ta nie leży „między swoimi punktami”, lecz jest nieograniczona. Euklides odróżniał jednak proste od odcinków, pisząc o „liniach przedłużanych w nieskończoność”, np.

„Linie równoległe są to proste, które leżą na tej samej płaszczyźnie i przedłużone z obu stron w nieskończoność, z żadnej strony nie przetną się”^[9].

Było to spowodowane próbą ominięcia trudności związanych z nieskończonością aktualną (prosta jako całość jest „nieskończona”) poprzez wyrażenie jej jako nieskończoność potencjalną (możliwość nieograniczonego przedłużania odcinka).

W starożytnej Grecji nie rozważano pojęcia nieskończoności, nastąpiło to dopiero w 1638, gdy Galileusz w swojej pracy „Discorsi” opisał linię jako składającą się z nieskończenie wielu punktów^[10].

Własności

• Przez dwa nieidentyczne punkty przestrzeni przechodzi tylko jedna prosta.
• Prosta przechodząca przez dwa różne punkty płaszczyzny zawiera się w tej płaszczyźnie.
• Prosta na płaszczyźnie jest zbiorem punktów jednakowo oddalonych od dwóch ustalonych punktów.
• Każdy punkt płaszczyzny lub przestrzeni należy do nieskończenie wielu prostych. Ich zbiór zwany jest pękiem prostych.
• Każda prosta dzieli płaszczyznę, w której się zawiera, na dwa obszary (półpłaszczyzny) i jest brzegiem każdego z nich.
• Każdy punkt na prostej dzieli ją na dwie części zwane półprostymi.
• Najkrótsza^[11] droga pomiędzy dwoma dowolnymi punktami prowadzi po prostej.
• Prosta jest częścią wspólną dowolnych dwóch nierównoległych płaszczyzn (zob. rysunek).
• Promień krzywizny (dla większej liczby wymiarów – wszystkie promienie krzywizny) w każdym jej punkcie jest nieskończony.
• Proste są jedynymi krzywymi gładkimi o zerowej krzywiźnie w każdym punkcie.
• Każda prosta ma nieskończoną liczbę osi symetrii. Osią taką jest ona sama oraz każda prosta prostopadła do niej.

Niektóre ważne proste

• asymptota – prosta, do której dąży dana krzywa (w szczególności wykres funkcji)
• normalna – prosta prostopadła do stycznej w danym punkcie krzywej
• oś liczbowa – prosta skierowana z liczbą przyporządkowaną każdemu swojemu punktowi, używana np. jako oś współrzędnych
• oś obrotu – prosta, wokół której obraca się dane ciało, albo względem której dokonujemy obrotu matematycznej bryły
• prosta Cevy – prosta przechodząca przez wierzchołek trójkąta i przeciwległy bok.
• prosta Eulera
• prosta potęgowa – zbiór punktów, które mają równe potęgi względem dwóch różnych okręgów
• sieczna – prosta przecinająca daną krzywą w co najmniej dwóch punktach
• styczna – potocznie i nieściśle: prosta „równoległa” do krzywej w danym punkcie i przechodząca przez ten punkt
• symetralna odcinka – prosta dzieląca odcinek na dwie równe części i prostopadła do niego
• oś symetrii – prosta, względem której można odbić daną figurę i otrzymać figurę identyczną
• środkowa – prosta łącząca wierzchołek trójkąta ze środkiem przeciwległego jego boku
• prosta Simsona

Prosta na płaszczyźnie (afinicznej)

Prosta jest jednowymiarową podprzestrzenią afiniczną płaszczyzny dwuwymiarowej (i ogólniej, każdej n-wymiarowej kartezjańskiej przestrzeni współrzędnych).

Jeśli dany jest punkt ${\displaystyle B}$ i niezerowy wektor ${\displaystyle {\overrightarrow {\alpha }},}$ to prostą generowaną przez wektor ${\displaystyle {\overrightarrow {\alpha }}}$ i przechodzącą przez punkt ${\displaystyle B}$ nazywamy zbiór punktów ${\displaystyle P}$ dla których istnieje liczba rzeczywista ${\displaystyle t}$ taka, że

${\displaystyle {\overrightarrow {BP}}=t{\overrightarrow {\alpha }}.}$

Wektor ${\displaystyle {\overrightarrow {\alpha }}}$ nazywamy wektorem kierunkowym prostej.

Najmniejszą^[12] podprzestrzenią afiniczną zawierającą dwa różne punkty ${\displaystyle P,Q}$ jest prosta, która przez nie przechodzi. Prostą tę oznaczamy ${\displaystyle {\text{af}}(P,Q).}$

Prostą można określić jako zbiór punktów spełniających pewne równanie liniowe. Równanie to można zapisać w różny sposób. Kilka typowych zapisów podano poniżej.

Równanie ogólne

W przestrzeni kartezjańskiej dwuwymiarowej każda prosta może być zdefiniowana w następujący sposób:

Dla pewnych liczb rzeczywistych ${\displaystyle A,B,C,}$ przy czym ${\displaystyle A}$ i ${\displaystyle B}$ nie są jednocześnie równe zeru, prosta to zbiór punktów, których współrzędne spełniają zależność^[13]:

${\displaystyle Ax+By+C=0.}$

Równanie to nazywamy równaniem ogólnym prostej. Wektor o współrzędnych ${\displaystyle [-B,A]}$ jest wektorem kierunkowym prostej. Jest on do tej prostej równoległy. Wektor ${\displaystyle [A,B]}$ jest prostopadły do prostej. Jeśli ${\displaystyle A=0,}$ to prosta jest równoległa do osi ${\displaystyle Ox,}$ jeśli ${\displaystyle B=0}$ – do osi ${\displaystyle Oy,}$ jeśli ${\displaystyle C=0,}$ przechodzi przez początek układu współrzędnych^[13].

Współczynniki ${\displaystyle A}$ i ${\displaystyle B}$ nie mogą równocześnie być równe zeru, gdyż wtedy równanie nie opisuje prostej, lecz dla ${\displaystyle C=0}$ całą płaszczyznę, a dla ${\displaystyle C\neq 0}$ zbiór pusty (nie ma rozwiązań).

Jedna prosta może mieć wiele różnych równań ogólnych, odpowiadających różnym równoległym wektorom kierunkowym. Współczynniki tych równań spełniają wtedy zależność:

${\displaystyle {\frac {A_{1}}{A_{2}}}={\frac {B_{1}}{B_{2}}}={\frac {C_{1}}{C_{2}}}}$

lub jeśli któryś z mianowników jest zerem, odpowiadający mu licznik także jest zerem.

Równanie normalne

Równanie ogólne można unormować, dzieląc współczynniki ${\displaystyle A,}$ ${\displaystyle B}$ i ${\displaystyle C}$ przez długość (normę) wektora kierunkowego i wybierając arbitralnie jeden z dwóch możliwych zwrotów tego wektora, np. tak jak poniżej^[14]:

${\displaystyle {\begin{cases}A'=A\mu \\B'=B\mu \\C'=C\mu \end{cases}},}$

gdzie ${\displaystyle \mu }$ to tzw. czynnik normujący:

${\displaystyle \mu ={\frac {1}{\sqrt {A^{2}+B^{2}}}}}$ dla ${\displaystyle C<0}$

lub

${\displaystyle \mu ={\frac {-1}{\sqrt {A^{2}+B^{2}}}}}$ dla ${\displaystyle C>0.}$

Dla ${\displaystyle C=0}$ można przyjąć dowolny znak.

Otrzymujemy w ten sposób tzw. równanie normalne, czyli równanie prostej położonej pod kątem ${\displaystyle \alpha }$ do osi ${\displaystyle Oy}$ i odległej o ${\displaystyle p}$ od środka układu współrzędnych:

${\displaystyle x\cos \alpha +y\sin \alpha -p=0,}$

przy czym ${\displaystyle 0\leqslant \alpha <2\pi .}$

Równanie normalne jednoznacznie identyfikuje prostą nie przechodzącą przez początek układu współrzędnych. Dla prostej przechodzącej przez początek układu wciąż możliwe są dwa różne równania normalne różniące się znakiem ${\displaystyle A}$ i ${\displaystyle B}$ (${\displaystyle C}$ jest wtedy zerem). Ponadto dla równania normalnego upraszczają się podane dalej wzory dotyczące kąta między dwiema prostymi.

Równanie w postaci kierunkowej

Jeśli prosta nie jest równoległa do osi rzędnych (Oy), równanie prostej można zapisać w tzw. postaci kierunkowej^[13]:

${\displaystyle y=ax+b,}$

gdzie ${\displaystyle a}$ i ${\displaystyle b}$ to liczby rzeczywiste.

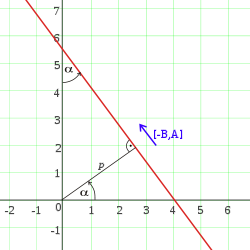
• ${\displaystyle a,}$ tzw. współczynnik kierunkowy, jest równy tangensowi kąta między prostą a osią odciętych (OX) nazywanego kątem nachylenia prostej^[13][15]. Czasem ten współczynnik jest oznaczany literą ${\displaystyle m.}$ Dwie proste o tym samym współczynniku kierunkowym są równoległe. Czerwona i niebieska prosta na wykresie mają ten sam współczynnik kierunkowy.
• ${\displaystyle b,}$ tzw. wyraz wolny, jest rzędną punktu, w którym prosta przecina oś rzędnych. Proste czerwona i zielona na wykresie mają ten sam wyraz wolny.

Równanie parametryczne

Prosta ${\displaystyle l}$ o (niezerowym) wektorze kierunkowym ${\displaystyle {\overrightarrow {\alpha }}=[u_{1},u_{2}],}$ przechodząca przez punkt ${\displaystyle A=(x_{A},y_{A})}$ to zbiór punktów ${\displaystyle P=(x,y),}$ takich że

${\displaystyle P=A+t{\overrightarrow {\alpha }}}$ dla dowolnych ${\displaystyle t\in \mathbb {R} .}$

Innymi słowy:

${\displaystyle l=\{A+t{\overrightarrow {\alpha }}\colon t\in \mathbb {R} \}.}$

W nowoczesnej geometrii analitycznej oznacza się to:

${\displaystyle l=A+{\text{lin}}({\overrightarrow {\alpha }}).}$

Rozpisując poszczególne składowe, możemy to samo równanie przedstawić za pomocą układu równań postaci:

${\displaystyle {\begin{cases}x=x_{A}+tu_{1}\\y=y_{A}+tu_{2}\end{cases}}.}$

Przy tym ${\displaystyle x_{A}}$ i ${\displaystyle y_{A}}$ są dowolnymi liczbami rzeczywistymi, natomiast ${\displaystyle u_{1}}$ i ${\displaystyle u_{2}}$ są także liczbami rzeczywistymi, które jednak nie mogą być jednocześnie równe zeru. Wówczas bowiem układ równań opisywałby tylko pojedynczy punkt ${\displaystyle A,}$ a nie całą prostą.

Równanie kanoniczne

Pod założeniami z poprzedniego ustępu, prostą ${\displaystyle l}$ można opisać równaniem:

${\displaystyle l\colon {\frac {x-x_{A}}{u_{1}}}={\frac {y-y_{A}}{u_{2}}}.}$

W przypadku, gdy ${\displaystyle u_{1}}$ lub ${\displaystyle u_{2}}$ jest zerem, przydatne może być zapisanie równania w postaci:

${\displaystyle (x-x_{A})u_{2}=(y-y_{A})u_{1}.}$

Równanie prostej przechodzącej przez zadane punkty

Gdy dane są dwa różne punkty ${\displaystyle (x_{A},y_{A})}$ i ${\displaystyle (x_{B},y_{B}),}$ to równanie prostej przez nie przechodzącej jest postaci^[13]:

${\displaystyle (y-y_{A})(x_{B}-x_{A})-(y_{B}-y_{A})(x-x_{A})=0}$

lub w wersji parametrycznej:

${\displaystyle {\begin{cases}x=x_{A}+t(x_{B}-x_{A})\\y=y_{A}+t(y_{B}-y_{A})\end{cases}},}$

gdzie ${\displaystyle t}$ przebiega wszystkie liczby rzeczywiste.

To samo równanie można przedstawić w postaci wyznacznika:

${\displaystyle {\begin{vmatrix}x&y&1\\x_{A}&y_{A}&1\\x_{B}&y_{B}&1\end{vmatrix}}=0.}$

Dla równania ogólnego: ${\displaystyle Ax+By+C=0}$ będziemy mieli

${\displaystyle {\begin{cases}A=y_{B}-y_{A}\\B=x_{A}-x_{B}\\C=x_{B}\cdot y_{A}-x_{A}\cdot y_{B}\end{cases}}.}$

Sprawdzenie, czy punkt (x,y) leży na linii

Dla równania ogólnego należy po prostu sprawdzić, czy ${\displaystyle A\cdot x+B\cdot y+C=0,}$ a w praktyce ${\displaystyle \left|A\cdot x+B\cdot y+C\right|<\epsilon .}$

Sprawdzenie równoległości albo punktu przecinania się dwóch linii

Dostajemy albo wyliczamy postać normalną: ${\displaystyle A_{1}x+B_{1}y+C_{1}=0,\ \ A_{2}x+B_{2}y+C_{2}=0,}$
Liczymy mianownik ${\displaystyle D=A_{1}*B_{2}-A_{2}*B_{1}.}$

Jeśli ${\displaystyle D=0}$ albo w praktyce ${\displaystyle \left|D\right|<\epsilon }$ linie są równoległe.
Jeśli linie nie są równoległe, liczymy punkt przecięcia (x,y):

${\displaystyle {\begin{cases}x=(B_{1}\cdot C_{2}-B_{2}\cdot C_{1})/D\\y=-(A1\cdot C2-A2\cdot C1)/D\end{cases}}.}$

Linia równoległa przechodząca przez zadany punkt

Dla linii ${\displaystyle Ax+By+C=0}$ jest ${\displaystyle Ax+By+C_{1}=0}$ z identycznymi A i B oraz C wyliczonym ze wzoru ${\displaystyle C=-(A\cdot x+B\cdot y).}$

Równanie odcinkowe

Równanie prostej przecinającej oś ${\displaystyle Ox}$ w punkcie ${\displaystyle (a,0),}$ gdzie ${\displaystyle a\neq 0}$ i oś ${\displaystyle Oy}$ w punkcie ${\displaystyle (0,b),}$ gdzie ${\displaystyle b\neq 0{:}}$

${\displaystyle {\frac {x}{a}}+{\frac {y}{b}}=1.}$

Postać biegunowa równania

Prostą można też wyrazić w biegunowym układzie współrzędnych ${\displaystyle (\varphi ,r).}$ Równanie prostej nie przechodzącej przez biegun przyjmuje wówczas postać

${\displaystyle r={\frac {p}{\cos(\varphi -\alpha )}},}$

gdzie:

• ${\displaystyle p}$ jest odległością prostej od bieguna,
• ${\displaystyle \alpha }$ to kąt między osią biegunową i półprostą poprowadzoną z bieguna prostopadle do danej prostej,
• ${\displaystyle r}$ jest współrzędną punktu prostej – odległością od bieguna,
• ${\displaystyle \varphi }$ jest współrzędną punktu prostej – kątem między osią biegunową i półprostą poprowadzoną z bieguna do danego punktu.

Jeśli prosta przechodzi przez biegun, to jej równanie ma postać ${\displaystyle \phi =\alpha +k\pi ,}$ gdzie:

• ${\displaystyle \alpha }$ to kąt między osią biegunową a prostą,
• ${\displaystyle k}$ jest dowolną liczbą całkowitą,
• ${\displaystyle r}$ – odległość od bieguna – może być wówczas dowolna.

Odległość punktu od prostej

 Osobny artykuł: Odległość punktu od prostej.

Odległość punktu ${\displaystyle P=(x_{P},y_{P})}$ od prostej danej równaniem ogólnym^[13]:

${\displaystyle d={\frac {|Ax_{P}+By_{P}+C|}{\sqrt {A^{2}+B^{2}}}}.}$

Odległość punktu ${\displaystyle P}$ od prostej danej równaniem normalnym:

${\displaystyle d=|x_{P}\cos \alpha +y_{P}\sin \alpha -p|.}$

Wyrażenie ${\displaystyle x_{P}\cos \alpha +y_{P}\sin \alpha -p}$ ma wartość dodatnią, gdy punkt ${\displaystyle P}$ oraz początek układu współrzędnych leżą po przeciwnych stronach danej prostej, ujemną – jeśli leżą po tej samej stronie, i zero, jeśli ${\displaystyle P}$ leży na prostej.

Wzajemne położenie na płaszczyźnie

Dla prostych ${\displaystyle k,l}$ danych równaniami

${\displaystyle k\colon A_{1}x+B_{1}y+C_{1}=0,\;l\colon A_{2}x+B_{2}y+C_{2}=0}$

niech:

${\displaystyle W_{AB}={\begin{vmatrix}A_{1}&B_{1}\\A_{2}&B_{2}\end{vmatrix}}=A_{1}B_{2}-A_{2}B_{1},}$

${\displaystyle W_{BC}={\begin{vmatrix}B_{1}&C_{1}\\B_{2}&C_{2}\end{vmatrix}}=B_{1}C_{2}-B_{2}C_{1},}$

${\displaystyle W_{CA}={\begin{vmatrix}C_{1}&A_{1}\\C_{2}&A_{2}\end{vmatrix}}=C_{1}A_{2}-C_{2}A_{1}.}$

Jeśli ${\displaystyle W_{AB}\neq 0,}$ wówczas proste ${\displaystyle k,l}$ przecinają się w punkcie

${\displaystyle \left({\frac {W_{BC}}{W_{AB}}},{\frac {W_{CA}}{W_{AB}}}\right).}$

Jeśli ${\displaystyle W_{AB}=0,}$ ale ${\displaystyle W_{BC}\neq 0}$ to zachodzi także ${\displaystyle W_{CA}\neq 0}$ i proste ${\displaystyle k,l}$ są równoległe.

Jeśli ${\displaystyle W_{AB}=W_{BC}=0,}$ to również ${\displaystyle W_{CA}=0}$ i proste pokrywają się ${\displaystyle (k=l)}$ (równania opisują ten sam zbiór punktów); współczynniki prostych spełniają wówczas zależność:

${\displaystyle {\frac {A_{1}}{A_{2}}}={\frac {B_{1}}{B_{2}}}={\frac {C_{1}}{C_{2}}}}$

lub jeśli któryś z mianowników tego równania jest zerem, odpowiadający mu licznik także jest zerem.

Kąt między dwiema prostymi

Kąt pomiędzy dwiema prostymi jest wyznaczony przez półproste, których początek znajduje się w punkcie przecięcia prostych.

Kąt ${\displaystyle \varphi }$ między prostymi na płaszczyźnie, zadanymi równaniami

${\displaystyle A_{1}x+B_{1}y+C_{1}=0,\ \ A_{2}x+B_{2}y+C_{2}=0,}$

daje się wyznaczyć ze wzorów

${\displaystyle \operatorname {tg} \varphi ={\frac {A_{1}B_{2}-A_{2}B_{1}}{A_{1}A_{2}+B_{1}B_{2}}},}$

${\displaystyle \cos \varphi ={\frac {A_{1}A_{2}+B_{1}B_{2}}{{\sqrt {A_{1}^{2}+B_{1}^{2}}}{\sqrt {A_{2}^{2}+B_{2}^{2}}}}},}$

${\displaystyle \sin \varphi ={\frac {A_{1}B_{2}-A_{2}B_{1}}{{\sqrt {A_{1}^{2}+B_{1}^{2}}}{\sqrt {A_{2}^{2}+B_{2}^{2}}}}}.}$

Wzory te upraszczają się, jeśli równania prostych są unormowane.

Można też użyć wzorów dla dwóch szczególnych przypadków:

• jeśli ${\displaystyle A_{1}B_{2}-A_{2}B_{1}=0,}$ to proste są równoległe,
• jeśli ${\displaystyle A_{1}A_{2}+B_{1}B_{2}=0,}$ to są prostopadłe.

Zobacz też uogólnienia: kąt między dwiema krzywymi, kąt między prostymi w przestrzeni.

Trzy punkty na prostej

Trzy punkty ${\displaystyle (x_{1},y_{1}),\ (x_{2},y_{2}),\ (x_{3},y_{3})}$ leżą na jednej prostej (są współliniowe) wtedy i tylko wtedy, gdy

${\displaystyle {\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}=0.}$

Inny warunek konieczny i wystarczający współliniowości:

${\displaystyle {\frac {x_{3}-x_{1}}{x_{2}-x_{1}}}={\frac {y_{3}-y_{1}}{y_{2}-y_{1}}}}$

(lub jeśli któryś z mianowników tego równania jest zerem, odpowiadający mu licznik także jest zerem).

Trzy proste przecinające się w jednym punkcie

Jeśli proste o równaniach odpowiednio:

${\displaystyle A_{1}x+B_{1}y+C_{1}=0,}$

${\displaystyle A_{2}x+B_{2}y+C_{2}=0}$

przecinają się w punkcie ${\displaystyle P,}$ to prosta o równaniu

${\displaystyle A_{3}x+B_{3}y+C_{3}=0,}$

także przecina się z nimi w tym punkcie wtedy i tylko wtedy, gdy:

${\displaystyle {\begin{vmatrix}A_{1}&B_{1}&C_{1}\\A_{2}&B_{2}&C_{2}\\A_{3}&B_{3}&C_{3}\end{vmatrix}}=0.}$

Pęki prostych

Zbiór wszystkich prostych przechodzących przez dany (ustalony) punkt nazywamy pękiem prostych, a dany punkt środkiem pęku. Środek pęku może być zadany wprost lub jako punkt przecięcia dwóch prostych. Równanie pęku prostych o środku wyznaczonym przez nierównoległe proste zapisujemy w postaci:

${\displaystyle t_{1}(A_{1}x+B_{1}y+C_{1})+t_{2}(A_{2}x+B_{2}y+C_{2})=0,}$ gdzie ${\displaystyle t_{1},t_{2}\in \mathbb {R} }$ spełniają warunek ${\displaystyle t_{1}^{2}+t_{2}^{2}>0.}$

Każda prosta przechodząca przez środek pęku (będąca współpękowa z wszystkimi prostymi przechodzącymi przez ten punkt) da się przedstawić powyższym równaniem i, na odwrót, każde równanie powyższej postaci przedstawia pewną prostą należącą do pęku.

Zbiór prostych równoległych na płaszczyźnie (o wspólnym wektorze kierunkowym) nazywamy kierunkiem albo niewłaściwym pękiem prostych.

Przestrzeń trójwymiarowa

Równania określające prostą w przestrzeni trójwymiarowej łatwo otrzymać z podanych poniżej równań dla przestrzeni wielowymiarowej. Należy tylko, zgodnie z tradycją, zamiast ${\displaystyle x_{1},x_{2},x_{3}}$ napisać odpowiednio ${\displaystyle x,y,z}$ i przyjąć liczbę wymiarów ${\displaystyle n=3.}$

Przestrzeń wielowymiarowa

Dwie proste na płaszczyźnie mogą być albo równoległe (szczególnym przypadkiem są proste identyczne), albo przecinać się (czyli mieć jeden punkt wspólny). Dwie proste w przestrzeni trójwymiarowej (oraz dla większej liczby wymiarów) oprócz tego mogą być skośne, czyli nie przecinać się, ale nie być też równoległe.

Każde równanie w układzie równań liniowych z niewiadomymi będącymi liczbami rzeczywistymi zmniejsza o jeden maksymalną liczbę wymiarów zbioru rozwiązań układu. Aby więc opisać twór jednowymiarowy (prostą) w przestrzeni o ${\displaystyle n}$ wymiarach, trzeba użyć układu ${\displaystyle n-1}$ równań liniowych. Czasem można ten układ łatwo zapisać jako jedno równanie wektorowe.

We wszystkich poniższych wzorach indeksy dolne oznaczają kolejne współrzędne przestrzeni wielowymiarowej, a punkty definiowanej prostej mają współrzędne postaci ${\displaystyle (x_{1},x_{2},\dots ,x_{n});}$ ${\displaystyle n}$ to liczba wymiarów przestrzeni.

Równanie parametryczne

W przestrzeni kartezjańskiej n-wymiarowej najwygodniej określać prostą za pomocą równania parametrycznego.

W tym ujęciu prosta ${\displaystyle l}$ o (niezerowym) wektorze kierunkowym ${\displaystyle {\overrightarrow {\alpha }}=[u_{1},u_{2},\dots ,u_{n}],}$ przechodząca przez punkt ${\displaystyle A=(a_{1},\dots ,a_{n})}$ to zbiór punktów ${\displaystyle P=(x_{1},x_{2},\dots ,x_{n})}$ takich, że

${\displaystyle P=A+t{\overrightarrow {\alpha }},}$ dla dowolnych ${\displaystyle t\in \mathbb {R} .}$

Podobnie jak w poprzednich przypadkach, oznacza się to ${\displaystyle l=A+\operatorname {lin} ({\overrightarrow {\alpha }}).}$

Rozpisując poszczególne składowe, możemy to samo równanie przedstawić za pomocą układu równań postaci:

${\displaystyle {\begin{cases}x_{1}=a_{1}+tu_{1}\\x_{2}=a_{2}+tu_{2}\\\vdots \\x_{n}=a_{n}+tu_{n}\end{cases}}.}$

Przy tym ${\displaystyle a_{1},a_{2},\dots ,a_{n}}$ są dowolnymi liczbami rzeczywistymi, natomiast ${\displaystyle u_{1},u_{2},\dots ,u_{n}}$ są również liczbami rzeczywistymi, z których chociaż jedna musi być różna od zera. Inaczej bowiem prosta zdegenerowałaby się do punktu.

Równań w tym układzie jest ${\displaystyle n,}$ a nie ${\displaystyle n-1,}$ jak w pozostałych podejściach, gdyż wprowadzono kolejną zmienną ${\displaystyle t,}$ a więc konieczne jest n-te równanie, aby otrzymać prostą, a nie płaszczyznę.

Równania ogólne

Prosta w n-wymiarowej przestrzeni o współrzędnych może być opisana jako część wspólna ${\displaystyle n-1}$ hiperpłaszczyzn (dla przestrzeni trójwymiarowej po prostu dwóch płaszczyzn). Sprowadza się to do układu równań:

${\displaystyle {\begin{cases}a_{1,1}x_{1}+a_{1,2}x_{2}+\ldots +a_{1,n}x_{n}=D_{1}\\a_{2,1}x_{1}+a_{2,2}x_{2}+\ldots +a_{2,n}x_{n}=D_{2}\\\vdots \\a_{n-1,1}x_{1}+a_{n-1,2}x_{2}+\ldots +a_{n-1,n}x_{n}=D_{n-1}\end{cases}},}$

co w postaci macierzowej można zapisać jako

${\displaystyle {\begin{bmatrix}a_{1,1}&a_{1,2}&\ldots &a_{1,n}\\a_{2,1}&a_{2,2}&\ldots &a_{2,n}\\\vdots &\vdots &&\vdots \\a_{n-1,1}&a_{n-1,2}&\ldots &a_{n-1,n}\end{bmatrix}}\cdot {\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}}={\begin{bmatrix}D_{1}\\D_{2}\\\vdots \\D_{n-1}\end{bmatrix}}.}$

Układ ten opisuje prostą wtedy i tylko wtedy, gdy rząd macierzy

${\displaystyle {\text{r}}{\begin{bmatrix}a_{1,1}&a_{1,2}&\ldots &a_{1,n}\\a_{2,1}&a_{2,2}&\ldots &a_{2,n}\\\vdots &\vdots &&\vdots \\a_{n-1,1}&a_{n-1,2}&\ldots &a_{n-1,n}\end{bmatrix}}=n-1.}$

Równania kanoniczne

Prostą przechodzącą przez punkt ${\displaystyle P=(p_{1},p_{2},\dots ,p_{n})}$ i równoległą do wektora kierunkowego ${\displaystyle {\vec {u}}=[u_{1},u_{2},\dots ,u_{n}]}$ określają równania:

${\displaystyle {\frac {x_{1}-p_{1}}{u_{1}}}={\frac {x_{2}-p_{2}}{u_{2}}}=\ldots ={\frac {x_{n}-p_{n}}{u_{n}}}.}$

W przypadku ${\displaystyle n=3}$ to równanie można zapisać w postaci wektorowej:

${\displaystyle ({\vec {r}}_{x}-{\vec {r}}_{P})\times {\vec {u}}={\vec {0}},}$

gdzie wektor wodzący ${\displaystyle {\vec {r}}_{x}=[x_{1},x_{2},x_{3}]}$ i analogicznie ${\displaystyle {\vec {r}}_{P}=[p_{1},p_{2},p_{3}];}$ symbolem ${\displaystyle \times }$ oznaczono iloczyn wektorowy.

Można też te równania interpretować jako określające prostą przechodzącą przez punkt P i prostopadłej do hiperpłaszczyzny danej równaniem ${\displaystyle u_{1}x_{1}+u_{2}x_{2}+\ldots +u_{n}x_{n}+D=0.}$

Równania prostej przechodzącej przez zadane punkty

Gdy dane są dwa punkty ${\displaystyle (a_{1},\dots ,a_{n})}$ i ${\displaystyle (b_{1},\dots ,b_{n}),}$ to równania prostej przechodzącej przez te punkty są postaci:

${\displaystyle {\frac {x_{1}-a_{1}}{b_{1}-a_{1}}}={\frac {x_{2}-a_{2}}{b_{2}-a_{2}}}=\ldots ={\frac {x_{n}-a_{n}}{b_{n}-a_{n}}}.}$

Kąt między prostymi w przestrzeni

Kąt ${\displaystyle \varphi }$ między dwiema przecinającymi się prostymi, danymi za pomocą równań w postaci parametrycznej

${\displaystyle {\vec {r}}_{x}={\vec {r}}_{A}+t{\vec {u}}_{A},\ t\in \mathbb {R} }$

oraz

${\displaystyle {\vec {r}}_{x}={\vec {r}}_{B}+t{\vec {u}}_{B},\ t\in \mathbb {R} ,}$

wyraża wzór:

${\displaystyle \cos \varphi ={\frac {{\vec {u}}_{A}{\vec {u}}_{B}}{\|{\vec {u}}_{A}\|\cdot \|{\vec {u}}_{B}\|}}.}$

Symbol ${\displaystyle \|\cdot \|}$ oznacza normę (długość wektora), ${\displaystyle {\vec {u}}_{A}{\vec {u}}_{B}}$ oznacza iloczyn skalarny wektorów ${\displaystyle {\vec {u}}_{A}}$ i ${\displaystyle {\vec {u}}_{B}.}$

Jeśli proste nie przecinają się, wzór pokazuje kąt między prostymi po ich przesunięciu bez zmiany kierunków tak, aby się przecinały.

Jeśli proste przedstawimy w postaci parametrycznej: ${\displaystyle l_{1}=P_{1}+\operatorname {lin} ({\overrightarrow {\alpha }}_{1}),}$ ${\displaystyle l_{2}=P_{2}+\operatorname {lin} ({\overrightarrow {\alpha }}_{2}),}$ to miara kąta ${\displaystyle \varphi }$ między tymi prostymi wyraża się wzorem

${\displaystyle \cos \varphi ={\frac {{\overrightarrow {\alpha }}_{1}{\overrightarrow {\alpha }}_{2}}{\|{\overrightarrow {\alpha }}_{1}\|\cdot \|{\overrightarrow {\alpha }}_{2}\|}}.}$

Kąt między prostą a płaszczyzną

 Osobny artykuł: Kąt między prostą i płaszczyzną.

Geometrie nieeuklidesowe

 Osobny artykuł: Geometria nieeuklidesowa.

Euklides podał pięć postulatów, tworzących fundamenty jego geometrii^[16]. Szczególnie interesujący jest piąty z nich, tzw. postulat równoległości, który w oryginalnej wersji brzmiał

Jeśli prosta przecina dwie proste w ten sposób, że kąty wewnętrzne po tej samej stronie prostej przecinającej są mniejsze od dwóch kątów prostych to proste te (przecinane) spotkają się z tej właśnie strony. (Rysunek obok.)

Sformułowanie to było długie i stosunkowo mało oczywiste w porównaniu z innymi pewnikami, jednak było Euklidesowi niezbędne do przeprowadzenia wielu ważnych dowodów^[17]. Współczesnym Euklidesa nie udało się wyprowadzić go z pozostałych aksjomatów i w ten sposób usunąć z grona niezbędnych postulatów geometrii. Ostatecznie późniejsi matematycy odkryli, że pozostałe cztery postulaty nie są wystarczające dla aksjomatyzacji geometrii euklidesowej, da się jednak zastąpić piąty postulat prostszą, równoważną wersją, np.

Przez punkt nie leżący na danej prostej można przeprowadzić dokładnie jedną nie przecinającą jej prostą (czyli prostą równoległą).

Zmieniając sens tego postulatu, przy zachowaniu niezmienionych pozostałych, możemy uzyskać spójne i niesprzeczne systemy, tzw. geometrie nieeuklidesowe, które dobrze opisują przestrzeń zakrzywioną, np. geometrię powierzchni kuli.

Zasadniczo zmiany te mogą iść w dwóch różnych kierunkach:

• Przez punkt nie leżący na danej prostej można przeprowadzić więcej niż jedną prostą równoległą – otrzymujemy wówczas tzw. geometrię hiperboliczną (Łobaczewskiego)^[18].
• Przez punkt nie leżący na danej prostej nie można przeprowadzić żadnej prostej równoległej – otrzymujemy tzw. geometrię eliptyczną (sferyczną)^[19].

Można też wyobrazić sobie przestrzeń, która w niektórych obszarach ma właściwości geometrii hiperbolicznej, w innych geometrii eliptycznej, a w jeszcze innych euklidesowej – takie przestrzenie opisuje uogólnienie wszystkich tych geometrii, zwane geometrią Riemanna.

Proste w geometriach nieeuklidesowych nadal mogą być zdefiniowane jako nieograniczone linie geodezyjne danej przestrzeni, tak jak zasygnalizowano na początku artykułu. Tak zdefiniowane proste spełniają wszystkie aksjomaty Euklidesa, z wyjątkiem postulatu równoległości. Ta definicja pasuje także do geometrii euklidesowej, gdzie wyznacza zwykłe proste.

Geometria hiperboliczna (Łobaczewskiego)

 Osobny artykuł: Geometria hiperboliczna.

W geometrii hiperbolicznej przez punkt nie leżący na danej prostej przechodzą co najmniej dwie różne proste nie przecinające jej (zob. rysunek). W tej geometrii dla każdego kąta występuje też tzw. prosta zagradzająca kąt – prosta, która jest jednocześnie równoległa do obydwu jego ramion.

Istnieje kilka różnych modeli geometrii hiperbolicznej. Proste są w nich różnie interpretowane, jednak idzie za tym zmiana definicji pojęcia odległości:

• W modelu Kleina przestrzeń to wnętrze koła, a prosta to cięciwa tego koła.
• W modelu dysku Poincaré przestrzeń to także wnętrze koła, ale proste to części okręgów prostopadłe do obwodu tego koła w punktach styku, oraz średnice koła.
• W modelu półpłaszczyzny Poincaré przestrzeń to półpłaszczyzna z wyłączonym brzegiem, a proste to półokręgi o środkach na brzegu półpłaszczyzny oraz półproste prostopadłe do tego brzegu i zaczynające się na nim.
• W modelu Minkowskiego przestrzeń to jedna z powłok hiperboloidy dwupowłokowej, a proste to przecięcia tej powłoki z płaszczyznami przechodzącymi przez środek symetrii hiperboloidy.

Geometria eliptyczna (sferyczna)

 Osobny artykuł: Geometria eliptyczna.

W geometrii sferycznej, której model stanowi powierzchnia kuli (także kuli ziemskiej) nie istnieją dwie proste nie przecinające się. Punktami w tej geometrii są zbiory dwóch punktów euklidesowych leżących po przeciwnej stronie sfery, a prostymi tzw. okręgi wielkie^[20] sfery, czyli okręgi na jej powierzchni, których środek pokrywa się ze środkiem sfery.

Przykładowe okręgi wielkie na rysunku obok są oznaczone ciągłymi liniami. Inne okręgi (oznaczone przerywanymi liniami) nie są prostymi tej geometrii, gdyż nie wyznaczają najkrótszych dróg. Pomiędzy dwoma dowolnymi punktami sfery można bowiem przejść po łukach nieskończonej liczby różnych okręgów, ale tylko jeden z tych okręgów będzie okręgiem wielkim, i ta właśnie trasa będzie najkrótsza – jest to tak zwana ortodroma. Z definicji zatem łuki okręgów wielkich to odcinki w geometrii sferycznej, łuki pozostałych okręgów odcinkami nie są.

Wprowadzając dla dwuwymiarowej geometrii eliptycznej układ współrzędnych z długością geograficzną ${\displaystyle \phi }$ i szerokością geograficzną ${\displaystyle \theta ,}$ możemy zdefiniować jej prostą (okrąg wielki) równaniem:

${\displaystyle A\cos \theta \cos \phi +B\cos \theta \sin \phi +C\sin \theta =0,}$

gdzie ${\displaystyle A,}$ ${\displaystyle B}$ i ${\displaystyle C}$ są dowolnymi liczbami rzeczywistymi, które nie są jednocześnie wszystkie trzy równe zeru.

Sfera jest przykładem przestrzeni ograniczonej, w której proste również są ograniczone. Jednak nawet tutaj okręgi wielkie pozostają liniami geodezyjnymi i nie posiadają zakończeń.

Czasoprzestrzeń

W tej sekcji występują konwencje związane z teoriami relatywistycznymi.

W szczególnej oraz ogólnej teorii względności przestrzeń fizyczna i czas są związane, tworząc w sensie matematycznym czterowymiarową czasoprzestrzeń. W szczególnej teorii względności czasoprzestrzeń ta jest przestrzenią Minkowskiego, a w ogólnej teorii względności przestrzenią pseudoriemannowską będącą modyfikacją geometrii Riemanna. W obydwu teoriach linia świata ciała na które nie działa żadna siła jest linią prostą (geodezyjną). W ogólnej teorii względności grawitacji nie uznaje się za oddziaływanie, lecz czynnik, który zakrzywia czasoprzestrzeń^{[potrzebny przypis]}. Ciało oddziaływające grawitacyjnie nadal przemieszcza się po prostej (analogicznie do pierwszej zasady dynamiki Newtona), jednak nie jest to prosta przestrzeni fizycznej, lecz prosta w zakrzywionej czasoprzestrzeni. Stąd z punktu widzenia geometrii euklidesowej porusza się ono (w przestrzeni fizycznej) po zakrzywionym torze. Grawitacja nie jest interpretowana jako siła działająca na ciało, a jako zakrzywienie czasoprzestrzeni, w której to ciało się porusza^[21].

Wzajemne położenie punktów w czasoprzestrzeni jest dzielone na trzy typy w zależności od wartości interwału czasoprzestrzennego (odpowiednik odległości). Ponieważ wszystkie punkty prostej w czasoprzestrzeni mają ten sam typ, proste także możemy podzielić na:

• czasowe (interwał czasoprzestrzenny ${\displaystyle s_{12}^{2}>0;}$ proste reprezentują prędkości mniejsze od prędkości światła w próżni) – mogą być trajektoriami cząstek posiadających niezerową masę spoczynkową;
• zerowe (${\displaystyle s_{12}^{2}=0;}$ proste reprezentują prędkość światła c) – mogą być trajektoriami jedynie cząstek bezmasowych (np. fotonów);
• przestrzenne (${\displaystyle s_{12}^{2}<0;}$ proste reprezentują prędkości większe od c) – nie mogą być trajektoriami żadnych cząstek (oprócz hipotetycznych tachionów, których istnienie nie zostało w żaden sposób potwierdzone).

Krzywa ${\displaystyle x^{\alpha }(s),}$ która ma w punkcie ${\displaystyle s}$ kierunek ${\displaystyle dx^{\alpha }/ds=U^{\alpha }(s)}$ jest linią geodezyjną (prostą w czasoprzestrzeni) jeśli

${\displaystyle \nabla _{U}U^{\beta }=0}$

lub

${\displaystyle U^{\alpha }\nabla _{\alpha }U^{\beta }=0,}$

co oznacza, że jej pochodna kowariantna dla jej kierunku w danym punkcie jest równa zeru.

Inne przestrzenie i geometrie

Przestrzeń liniowa (wektorowa)

 Osobny artykuł: Przestrzeń liniowa.

W tym ujęciu prosta jest jednowymiarową przestrzenią liniową. Dokładniej, prosta jest tożsama z jednowymiarową podprzestrzenią przestrzeni liniowej rozpiętej nad ciałem liczb rzeczywistych.

Jeśli ${\displaystyle {\vec {U}}}$ jest wektorem niezerowym, to prosta jest zbiorem wektorów ${\displaystyle {\vec {W}},}$ dla których istnieje skalar ${\displaystyle k}$ (rzeczywisty dla przestrzeni wektorowej należącej do ${\displaystyle \mathbb {R} }$) taki, że ${\displaystyle {\vec {W}}=k{\vec {U}}.}$ Mówimy, że wektory ${\displaystyle {\vec {U}}}$ i ${\displaystyle {\vec {W}}}$ są liniowo zależne lub współliniowe.

Przestrzeń metryczna

 Osobny artykuł: Przestrzeń metryczna.

W przestrzeni metrycznej naturalnym uogólnieniem prostych są linie geodezyjne, jak podano na wstępie.

Geometria rzutowa

 Osobny artykuł: Geometria rzutowa.

Geometria rzutowa bada własności figur geometrycznych, które nie zmieniają się pod wpływem tzw. przekształceń rzutowych, czyli dla płaszczyzny przekształceń, które przekształcają proste zawsze w proste (a nie w inne obiekty).

W geometrii rzutowej mamy dwa rodzaje prostych:

• proste właściwe – każda prosta właściwa jest zbiorem punktów zwykłej prostej z przestrzeni kartezjańskiej, uzupełnionym o jej kierunek zwany tu punktem w nieskończoności;
• prosta rzutowa – będąca zbiorem punktów w nieskończoności.

Takie ujęcie pozwala uzyskać szereg interesujących własności, np. dowolne dwie nie identyczne proste przecinają się zawsze w jednym punkcie.

Najelegantszym wynikiem geometrii rzutowej jest zasada dualności mówiąca, iż dowolne prawdziwe twierdzenie pozostaje w obrębie tej geometrii prawdziwe, jeśli zamienimy w nim pojęcia „prosta” i „punkt” (i odpowiednio „przechodzi przez” z „leży na”).

Geometria wykreślna

 Osobny artykuł: Geometria wykreślna.

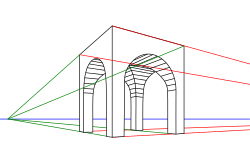
Geometria wykreślna jest szeroko używaną w technice i architekturze nauką stosowaną, zajmującą się sposobami jednoznacznego przedstawiania trójwymiarowych obiektów w formie rzutów prostokątnych na prostopadłe płaszczyzny ${\displaystyle \pi _{1}}$ i ${\displaystyle \pi _{2}}$ (tzw. rzutnie).

Proste odwzorowywane są następująco: przez daną prostą prowadzimy płaszczyzny ${\displaystyle \varepsilon _{1}}$ i ${\displaystyle \varepsilon _{2}}$ prostopadłe odpowiednio do rzutni ${\displaystyle \pi _{1}}$ i ${\displaystyle \pi _{2},}$ tzw. płaszczyzny rzutujące. Ich krawędzie przecięcia z rzutniami to właśnie rzuty poziomy i pionowy prostej.

Takie dwa rzuty prostej jednoznacznie ją identyfikują, z wyjątkiem przypadku prostej prostopadłej do osi ${\displaystyle x}$ i nierównoległej do żadnej z pozostałych osi. Jej rzuty są identyczne z rzutami dowolnej innej prostej na płaszczyźnie prostopadłej do osi ${\displaystyle x.}$ Aby jednoznacznie ją odwzorować, konieczne jest przedstawienie dodatkowo rzutów dwóch dowolnych jej punktów.

Jeśli prosta jest prostopadła do jednej z rzutni, jej rzut na tę rzutnię staje się punktem i zbędne staje się prowadzenie płaszczyzny prostopadłej do tej rzutni.

Niektóre proste mają szczególne nazwy ze względu na położenie względem rzutni:

• prosta pozioma – równoległa do rzutni poziomej ${\displaystyle \pi _{1};}$ jej punkty mają jednakową wysokość;
• prosta czołowa – równoległa do rzutni pionowej ${\displaystyle \pi _{2};}$ jej punkty mają jednakową głębokość;
• prosta pionowa – prostopadła do rzutni ${\displaystyle \pi _{1};}$ rzutem poziomym jest punkt;
• prosta celowa – prostopadła do rzutni ${\displaystyle \pi _{2};}$ rzutem pionowym jest punkt.

Zobacz też

 Wykaz literatury uzupełniającej: Prosta.

• aksjomat Archimedesa
• Elementy – dzieło Euklidesa
• ewolwenta
• geometria wykreślna
• kolineacja
• konstrukcje geometryczne
• krzywa
• odcinek
• perspektywa
• powierzchnia prostokreślna
• półprosta
• przekształcenie liniowe
• przekształcenie afiniczne
• punkt
• rzut prostokątny
• rzut równoległy
• twierdzenie Cevy
• twierdzenie o trzech prostopadłych
• wskaźniki Millera

Przypisy

Bibliografia

• Andrzej Szczepan Białynicki-Birula: Algebra liniowa z geometrią. Warszawa: PWN, 1976, seria: Biblioteka Matematyczna. ISBN 83-01-00171-2.brak strony w książce
• Franciszek Otto, Edward Otto: Podręcznik geometrii wykreślnej. Warszawa: PWN, 1975. ISBN 978-83-01-00933-5.brak strony w książce
• Wanda Szmielew: Od geometrii afinicznej do euklidesowej: rozważania nad aksjomatyką. Warszawa: PWN, 1983. ISBN 83-01-03513-7.brak strony w książce
• Hans Niels Jahnke: A history of analysis. Providence, RI: American Mathematical Society, 2003. ISBN 0-8218-2623-9. OCLC 51607350.

Większość wzorów w tym artykule pochodzi z:

• Igor N. Bronsztejn, Konstantin A. Siemiendiajew: Matematyka, poradnik encyklopedyczny. Wyd. VI. Warszawa: PWN, 1976.

Linki zewnętrzne

Informacje w projektach siostrzanych

Cytaty w Wikicytatach

Definicje słownikowe w Wikisłowniku

• Applet pokazujący różne równania prostej na płaszczyźnie
• Marceli Stark: Geometria analityczna, Monografie Matematyczne, Tom 26. [w:] Biblioteka Wirtualna Nauki ICM [on-line]. Warszawa-Wrocław, 1951.
• Proste na płaszczyźnie