Propagatore

In meccanica quantistica e in teoria quantistica dei campi, il propagatore fornisce l'ampiezza di probabilità che una particella viaggi da un luogo ad un altro in un dato tempo, ovvero anche con una certa energia e momento. Il propagatore può essere visto come l'inverso dell'operatore d'onda appropriato per la particella e per questo è spesso identificato con la funzione di Green.

Nelle teorie in cui sono presenti dei campi in interazione, il propagatore è esprimibile tramite una rappresentazione spettrale, detta di Källén-Lehmann, che contiene un termine proporzionale alla funzione di Green dell'equazione in assenza di interazioni, con un polo legato alla massa fisica della particella del campo e che descrive quindi la propagazione di una singola particella, e un termine senza poli che descrive i contributi al propagatore dati da stati a più particelle, con una massa invariante maggiore di quella della particella del campo.

Si noti che nel calcolo delle ampiezze dei processi fisici i propagatori sono integrati su tutto lo spazio-tempo; ciò implica che, almeno su corte distanze, esistono ampiezze di probabilità per la propagazione di particelle da un qualunque punto dello spazio-tempo a qualunque altro. All'aumentare della distanza i contributi che dominano sono naturalmente quelli di tipo tempo per le particelle massive e quelli di tipo luce per le particelle a massa nulla.

Definizione

Nella meccanica quantistica non relativistica il propagatore fornisce la probabilità che una particella che si trova in un punto x dello spazio al tempo t, arrivi in un altro punto x' al tempo t'. È la funzione di Green dell'equazione di Schrödinger. Questo significa che se un sistema ha operatore hamiltoniano ${\displaystyle {\hat {H}}}$, il propagatore è una funzione ${\displaystyle K(x,t;x't')}$ tale che:

${\displaystyle \left({\hat {H}}_{x}-i\hbar {\frac {\partial }{\partial t}}\right)K(x,t;x',t')=-i\hbar \delta (x-x')\delta (t-t')}$

dove ${\displaystyle {\hat {H}}_{x}}$ indica l'hamiltoniano come funzione delle coordinate ${\displaystyle x}$ e ${\displaystyle \delta (x,x')}$ è la delta di Dirac.
Il propagatore può anche essere espresso come:

${\displaystyle K(x,t;x',t')=\langle x|{\hat {U}}(t,t')|x'\rangle =\langle xt|x't'\rangle \ }$

dove ${\displaystyle {\hat {U}}(t,t')}$ è l'operatore di evoluzione temporale che trasla lo stato dal tempo t a t'.

Integrale sui cammini nella meccanica quantistica non relativistica

Il propagatore, nella meccanica quantistica, può essere anche ricavato usando l'integrale sui cammini:

${\displaystyle K(x,t;x',t')=\int \exp \left[{\frac {i}{\hbar }}\int _{t}^{t'}L({\dot {q}},q,t)dt\right]D[q(t)]}$

dove le condizioni al contorno dell'integrale sui cammini sono q(t)=x, q(t')=x'. ${\displaystyle L}$ indica la lagrangiana del sistema.

Essendo

${\displaystyle S=\int _{t}^{t'}\;L(q,{\dot {q}},t)dt}$

l'azione della lagrangiana, si ottiene

${\displaystyle K(x,t;x',t')=\int \exp \left[{\frac {i}{\hbar }}S[q(t)]\right]D[q(t)]}$

Essendo l'esponenziale un'autofunzione dell'operatore di integrazione, si può scrivere in definitiva:

${\displaystyle K(x,t;x',t')=N\exp \left[{\frac {i}{\hbar }}S[q(t)]\right]}$

dove N è un fattore di normalizzazione.
Nella meccanica quantistica non relativistica il propagatore permette di trovare lo stato del sistema in ogni istante di tempo:

${\displaystyle \psi (x,t)=\int _{-\infty }^{\infty }\psi (x',t')K(x,t;x',t')dx'}$

Se ${\displaystyle K(x,t;x',t')}$ dipende solo dalla differenza ${\displaystyle x-x'}$, tale integrale è la convoluzione dello stato iniziale e del propagatore.

Propagatori relativistici

In meccanica quantistica relativistica e in teoria quantistica dei campi i propagatori sono invarianti di Lorentz. Danno l'ampiezza per una particella che viaggia tra i due punti dello spaziotempo.

Propagatore scalare

In teoria quantistica dei campi, la teoria di un campo scalare libero (non interagente) è un esempio semplice e utile che serve a illustrare i concetti necessari per teorie più complicate. Descrive particelle di spin 0. Ci sono una serie di possibili propagatori per la teoria di campo scalare libero.

Spazio delle posizioni

I propagatori nello spazio delle posizioni sono le funzioni di Green per l'equazione di Klein-Gordon. Ciò significa che sono funzioni ${\displaystyle G(x,y)}$ che soddisfano

${\displaystyle (\square _{x}+m^{2})G(x,y)=-\delta (x-y)}$

dove:

• ${\displaystyle x,y}$ sono due punti nello spaziotempo di Minkowski.
• ${\displaystyle \square _{x}={\tfrac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}}$ è l'operatore d'alembertiano agente sulle coordinate ${\displaystyle x}$.
• ${\displaystyle \delta (x-y)}$ è la delta di Dirac.

(Come è tipico in teoria dei campi relativistica, la velocità della luce e la costante di Planck ridotta sono poste a 1.)

Bisogna restringersi allo spaziotempo di Minkowski 4-dimensionale. Si può effettuare una trasformata di Fourier dell'equazione per il propagatore, ottenendo

${\displaystyle \left(-p^{2}+m^{2}\right)G(p)=-1.}$

Questa equazione può essere invertita nel senso delle distribuzioni notando che l'equazione ${\displaystyle xf(x)=1}$ ha la soluzione,

${\displaystyle f(x)={\frac {1}{x\pm i\varepsilon }}={\frac {1}{x}}\mp i\pi \delta (x),}$

dove è implicito il limite per ${\displaystyle \varepsilon \to 0}$.

La soluzione è

${\displaystyle G(x,y)={\frac {1}{(2\pi )^{4}}}\int d^{4}p\,{\frac {e^{-ip(x-y)}}{p^{2}-m^{2}\pm i\varepsilon }}~,}$

dove

${\displaystyle p(x-y):=p_{0}(x^{0}-y^{0})-{\vec {p}}\cdot ({\vec {x}}-{\vec {y}})}$

è il prodotto scalare quadrivettoriale.

Le scelte diverse per come deformare l'integrazione di contorno nell'espressione di cui sopra portano a varie forme per il propagatore. La scelta del contorno è solitamente espressa in termine dell'integrale su ${\displaystyle p_{0}}$.

L'integranda ha quindi due poli in

${\displaystyle p_{0}=\pm {\sqrt {{\vec {p}}^{2}+m^{2}}}}$

quindi scelte diverse di evitare questi portano a propagatori diversi.

Propagatore di Feynman

Un contorno che va sotto il polo sinistro e sopra il polo destro dà il propagatore di Feynman, introdotto dal fisico Richard Feynman nel 1948.^[1]

Questa scelta di contorno è equivalente a calcolare il limite^[2]

${\displaystyle G_{F}(x,y)=\lim _{\varepsilon \to 0}{\frac {1}{(2\pi )^{4}}}\int d^{4}p\,{\frac {e^{-ip(x-y)}}{p^{2}-m^{2}+i\varepsilon }}={\begin{cases}-{\frac {1}{4\pi }}\delta (s)+{\frac {m}{8\pi {\sqrt {s}}}}H_{1}^{(1)}(m{\sqrt {s}})&s\geq 0\\-{\frac {im}{4\pi ^{2}{\sqrt {-s}}}}K_{1}(m{\sqrt {-s}})&s<0.\end{cases}}}$

Qui

${\displaystyle s:=(x^{0}-y^{0})^{2}-({\vec {x}}-{\vec {y}})^{2},}$

dove ${\displaystyle x,y}$ sono due punti nello spaziotempo, e il punto all'esponente è un prodotto scalare quadrivettoriale. Inoltre ${\displaystyle H_{1}^{(1)}}$sono funzioni di Hankel e ${\displaystyle K_{1}}$ è una funzione di Bessel modificata.

Questa espressione può essere ricavata direttamente dalla teoria di campo come il valore di aspettazione del vuoto del prodotto tempo-ordinato del campo scalare libero, cioè, il prodotto viene sempre preso in modo tale che l'ordinamento temporale dei punti di spaziotempo è lo stesso,

${\displaystyle {\begin{aligned}G_{F}(x-y)&=-i\langle 0|T(\Phi (x)\Phi (y))|0\rangle \\[4pt]&=-i\left\langle 0|\left[\Theta (x^{0}-y^{0})\Phi (x)\Phi (y)+\Theta (y^{0}-x^{0})\Phi (y)\Phi (x)\right]|0\right\rangle .\end{aligned}}}$

Questa espressione è invariante di Lorentz, a patto che i campi commutino tra loro quando i punti ${\displaystyle x,y}$ sono separati da un intervallo di tipo spazio.

Propagatori nello spazio degli impulsi

La trasformata di Fourier dei propagatori nello spazio delle posizioni può essere pensata come quei propagatori nello spazio degli impulsi. In questo spazio assumono una forma più semplice.

Sono spesso scritti con il termine ${\displaystyle \varepsilon }$ esplicito ma è inteso solo come promemoria per quale contorno usare. Questo termine è incluso per incorporare le condizioni al contorno e la causalità.

Per il quadrimpulso ${\displaystyle p}$, vengono riportati di seguito i propagatori ritardato, avanzato, e di Feynman nello spazio degli impulsi:

${\displaystyle {\tilde {G}}_{\text{rit}}(p)={\frac {1}{(p_{0}+i\varepsilon )^{2}-{\vec {p}}^{2}-m^{2}}}}$

${\displaystyle {\tilde {G}}_{\text{av}}(p)={\frac {1}{(p_{0}-i\varepsilon )^{2}-{\vec {p}}^{2}-m^{2}}}}$

${\displaystyle {\tilde {G}}_{F}(p)={\frac {1}{p^{2}-m^{2}+i\varepsilon }}.}$

Al fine di calcolare diagrammi di Feynman di solito conviene aggiungere un fattore ${\displaystyle -i}$, ma ci sono diverse convenzioni.

Sempre per quanto riguarda le convenzioni il segno davanti a ${\displaystyle m^{2}}$ può essere positivo o negativo a seconda della segnatura scelta: ${\displaystyle p^{2}+m^{2}}$ per (+,-,-,-) o ${\displaystyle p^{2}-m^{2}}$ per (-,+,+,+).

Elettrodinamica quantistica

Lo stesso argomento in dettaglio: Elettrodinamica quantistica.

Nell'elettrodinamica quantistica bisogna distinguere due propagatori fondamentali, quello dei campi di Dirac e quello dei fotoni. Le funzioni di Green dei due campi sono le seguenti:

${\displaystyle iS_{F\alpha \beta }(x-y)=(i\gamma ^{\mu }\partial _{\mu }+m)_{\alpha \beta }\int {\frac {{\text{d}}^{4}p}{(2\pi )^{4}}}{\frac {e^{-ip(x-y)}}{p^{2}-m^{2}+i\varepsilon }}=(i\gamma ^{\mu }\partial _{\mu }+m)_{\alpha \beta }i\Delta _{F}(x-y;m^{2})}$ (fermioni)

${\displaystyle iD_{F}^{\mu \nu }(x-y)=\int {\frac {{\text{d}}^{4}k}{(2\pi )^{4}}}e^{-ik(x-y)}{\frac {(-g^{\mu \nu }+(1-\xi ){\frac {k^{\mu }k^{\nu }}{k^{2}}})}{k^{2}+i\varepsilon }}=-g^{\mu \nu }i\Delta _{F}(x-y;0)+\dots }$ (fotoni)

dove m² è il quadrato della massa dell'elettrone, ${\displaystyle i\Delta _{F}(x-y;m^{2})}$ è il propagatore libero di un campo scalare con massa m² nello spazio diretto, le derivate parziali ${\displaystyle \partial _{\mu }}$ agiscono sulla coordinata x, ${\displaystyle g_{00}=1}$, ${\displaystyle g_{ii}=-1}$, ${\displaystyle \xi }$ è un parametro libero che permette di fissare la gauge (per esempio ${\displaystyle \xi =0}$, la gauge di Landau, oppure ${\displaystyle \xi =1}$, la gauge di Feynman), mentre i puntini rappresentano appunto i termini del propagatore che non contribuiscono alle ampiezze fisiche.

I propagatori dei campi in interazione sono convenientemente espressi in termini della rappresentazione spettrale di Källén-Lehmann, del propagatore:

${\displaystyle \langle 0|T\{\psi _{\alpha }(x){\bar {\psi }}_{\beta }(y)\}|0\rangle =Z_{2}iS_{\alpha \beta }(x-y;m^{2})+\int {\text{d}}M^{2}\left[\sigma _{1}(M^{2})i\gamma ^{\mu }\partial _{\mu }+\sigma _{2}(M^{2})M\right]_{\alpha \beta }i\Delta _{F}(x-y;M^{2})}$

${\displaystyle \langle 0|T\{A^{\mu }(x)A^{\dagger \nu }(y)\}|0\rangle =Z_{3}iD_{F}^{\mu \nu }(x-y;0)+\int {\text{d}}M^{2}\sigma _{3}(M^{2})iD_{F}^{\mu \nu }(x-y;M^{2})+\dots }$

In queste formule ${\displaystyle iS(x-y;m^{2})}$ e ${\displaystyle iD^{\mu \nu }(x-y;0)}$ sono i propagatori dei campi liberi (alla massa dell'elettrone, m², e a massa nulla per il fotone), ${\displaystyle Z_{2}}$ e ${\displaystyle Z_{3}}$ sono le costanti di rinormalizzazione dei campi, mentre ${\displaystyle \sigma _{1}}$, ${\displaystyle \sigma _{2}}$ e ${\displaystyle \sigma _{3}}$ sono le densità spettrali che "pesano" il propagatore ad una massa invariante maggiore di quella della particella libera. I puntini nel propagatore del fotone sono termini eliminabili in virtù della conservazione delle linee fermioniche esterne tra le quali il propagatore dei fotoni è sempre racchiuso nelle ampiezze fisiche. Il propagatore libero viene dai campi in e out, che possono creare dal vuoto solo stati a una particella, mentre le densità spettrali sono legate ai termini di interazione e connettono il vuoto a stati a più particelle.
Ciò spiega la presenza delle costanti di rinormalizzazione: mentre il campo in o out ha probabilità uno di creare uno stato a una particella dal vuoto, il campo in interazione ha una probabilità inferiore di farlo, poiché può creare anche un numero di maggiore di particelle (tramite l'interazione col campo elettromagnetico).

La forma analitica per il propagatore di un fotone, nello spazio degli impulsi e nello spazio vuoto, è:

${\displaystyle {\frac {-ig_{\mu \nu }}{k^{2}+i\varepsilon }};}$

con ${\displaystyle g_{\mu \nu }}$ (${\displaystyle g_{00}=1}$ e ${\displaystyle g_{ii}=-1}$ con ${\displaystyle i=1,2,3}$) che è il tensore metrico.

I propagatori (liberi) dei fermioni sono indicati con delle linee continue dritte, usualmente con una freccia "in avanti" per i fermioni o "all'indietro" per gli antifermioni; i propagatori dei fotoni nei diagrammi di Feynman vengono tradizionalmente indicati da una linea ondulata. Nelle figure sono rappresentati due esempi di diagrammi di Feynman: nella prima, un diagramma al prim'ordine contenente un propagatore fotonico racchiuso tra due linee esterne fermioniche; nella seconda, un diagramma al second'ordine contenente due propagatori fotonici, due linee esterne fermioniche e un loop di fermioni (formato da due propagatori).

• 
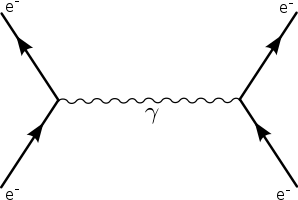  Diagramma di Feynman al primo ordine, contenente un propagatore fotonico.
• 
  Diagramma di Feynman al secondo ordine, contenente due propagatori fotonici e linee esterne fermioniche.

Teoria di Yang e Mills

Lo stesso argomento in dettaglio: Teoria di Yang-Mills.

Al fine di fornire una forma analitica per i propagatori dei bosoni vettoriali (valida anche per i bosoni vettori assiali), è importante ricordare che a differenza del caso elettromagnetico, nel quale la massa del fotone è nulla, per un bosone vettore si deve avere un termine di massa ${\displaystyle m}$. Si può dimostrare che il propagatore, nello spazio degli impulsi e nello spazio vuoto, è dato dalla seguente funzione:

${\displaystyle G_{\alpha \beta }(k)=i{\frac {-g_{\alpha \beta }+{\frac {k_{\alpha }k_{\beta }}{m^{2}}}}{k^{2}-m^{2}}}.}$

La funzione ${\displaystyle G_{\alpha \beta }(k)}$ genera un bosone vettore al tempo ${\displaystyle x'_{0}}$ e nella posizione ${\displaystyle {\textbf {x}}'}$ viene distrutta la stessa particella al tempo ${\displaystyle x_{0}}$ quando si trova in ${\displaystyle {\textbf {x}}}$ e pertanto il nostro bosone vettore si propaga da ${\displaystyle {\textbf {x}}'}$ a ${\displaystyle {\textbf {x}}}$.

Teoria a molti corpi

Lo stesso argomento in dettaglio: Teoria a molti corpi.

Nella teoria a molti corpi il propagatore elettronico del sistema non-interagente in uno spazio ${\displaystyle \mathbf {r} \omega }$ è dato dall'espressione:

${\displaystyle G^{(0)}(\mathbf {r} _{1},\mathbf {r} _{2};\omega )=\sum _{i}{\frac {\phi _{i}^{(0)}(\mathbf {r} _{1})\phi _{i}^{(0)*}(\mathbf {r} _{2})}{\omega -\varepsilon _{i}^{(0)}+i\eta \operatorname {sgn} \left(\varepsilon _{i}^{(0)}-\mu \right)}},}$

dove ${\displaystyle \varepsilon _{i}^{(0)},\phi _{i}^{(0)}(\mathbf {r} )}$ sono gli autovalori e autofunzioni dell'hamiltoniana ${\displaystyle H^{(0)}}$ del sistema non-interagente

${\displaystyle H^{(0)}\phi _{i}^{(0)}(\mathbf {r} )=\varepsilon ^{(0)}\phi _{i}^{(0)}(\mathbf {r} ),}$

ovverosia in un solido cristallino (${\displaystyle H^{(0)}}$ periodica) sono le bande e le funzioni di Bloch, in un atomo sono i livelli e le funzioni d'onda atomiche di particella singola, etc.

Note

Bibliografia

• Bjorken, J.D., Drell, S.D., Relativistic Quantum Fields (Appendix C.), New York: McGraw-Hill 1965, ISBN 0-07-005494-0.
• Edited by DeWitt, Cécile and DeWitt, Bryce, Relativity, Groups and Topology, (Blackie and Son Ltd, Glasgow), Especially p615-624, ISBN 0-444-86858-5
• Griffiths, David J., Introduction to Elementary Particles, New York: John Wiley & Sons, 1987. ISBN 0-471-60386-4
• Kerson Huang, Quantum Field Theory: From Operators to Path Integrals (New York: J. Wiley & Sons, 1998), ISBN 0-471-14120-8
• Itzykson, Claude, Zuber, Jean-Bernard Quantum Field Theory, New York: McGraw-Hill, 1980. ISBN 0-07-032071-3
• Pokorski, Stefan, Gauge Field Theories, Cambridge: Cambridge University Press, 1987. ISBN 0-521-36846-4 (Has useful appendices of Feynman diagram rules, including propagators, in the back.)
• Schulman, Larry S., Techniques & Applications of Path Integration, John Wiley & Sons (New York-1981) ISBN 0-471-76450-7

Voci correlate

• Bosone (fisica)
• Bosone vettore
• Bosoni vettori assiali
• Diagramma di Feynman
• Fotoni
• Lista delle particelle
• Self-energia
• Teoria a molti corpi
• Teoria di Yang-Mills

Collegamenti esterni

• Halliwell, J.J., Orwitz, M. Sum-over-histories origin of the composition laws of relativistic quantum mechanics and quantum cosmology, arXiv:gr-qc/9211004v2

V · D · M Teoria quantistica dei campi
Diagramma di Feynman · Storia della teoria quantistica dei campi
Premesse	Campo · Teoria classica dei campi · Teoria di gauge · Simmetria di Poincaré · Meccanica quantistica · Rottura spontanea di simmetria
Simmetria in fisica	Crossing · Coniugazione di carica · Parità · Simmetria temporale
Strumenti	Anomalia · Teoria di campo efficace · Valore di aspettazione del vuoto · Ghost di Faddeev-Popov · Diagramma di Feynman · Formule di riduzione LSZ · Funzione di partizione · Propagatore · Quantizzazione · Rinormalizzazione · Regolarizzazione · Vuoto quantistico · Teorema di Wick · Assiomi di Wightman
Equazioni	Equazione di Dirac · Equazione di Klein-Gordon · Equazione di Proca · Equazione di Wheeler-DeWitt
Modello standard	Interazione elettrodebole · Meccanismo di Higgs · Cromodinamica quantistica · Elettrodinamica quantistica · Teoria di Yang-Mills
Teorie incomplete	Gravità quantistica · Teoria delle stringhe · Supersimmetria · Technicolor · Teoria del tutto
Scienziati	Bethe · Bogoljubov · Callan · Coleman · DeWitt · Dirac · Dyson · Fermi · Feynman · Fierz · Fröhlich · Gell-Mann · Goldstone · Gross · Haag · 't Hooft · Jackiw · Klein · Landau · Lee · Lehmann · Majorana · Nambu · Parisi · Poljakov · Salam · Schwinger · Skyrme · Stueckelberg · Symanzik · Tomonaga · Veltman · Weinberg · Weisskopf · Wightman · Wilson · Witten · Yang · Yukawa · Wilczek · Zimmermann

Portale Fisica: accedi alle voci di Wikipedia che trattano di fisica