Pentagone régulier convexe

Cet article ne cite pas suffisamment ses sources (juillet 2021).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

Pentagone régulier convexe
Pentagone régulier convexe (en noir), son cercle circonscrit (en gris), les segments reliant son centre à ses sommets (en gris), et ses angles remarquables : angle interne (en noir), angle externe (en gris).
Type	Polygone régulier convexe
Arêtes	5
Sommets	5
Symbole de Schläfli	{5}
Diagramme de Coxeter-Dynkin
Groupe de symétrie	Diédral (D10)
Angle interne	108°
Propriétés	Constructible
modifier

En géométrie, un pentagone régulier convexe (ou plus simplement pentagone régulier, voire pentagone) est un pentagone convexe dont les cinq côtés ont la même longueur et dont les cinq angles internes ont la même mesure. Il est constructible à la règle et au compas.

Généralités

Propriétés

Le pentagone régulier convexe est un polygone régulier, c'est-à-dire équilatéral et équiangle. Par conséquent :

• il est isogonal, isotoxal et autodual ;
• il est bicentrique, c'est-à-dire à la fois
  • inscriptible : ses sommets sont cocycliques et
  • circonscriptible : il possède un cercle inscrit, c'est-à-dire qu'il existe un cercle tangent à chacun de ses côtés ;
• les cercles inscrit et circonscrit ont même centre.

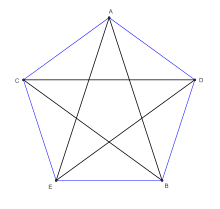
Il est convexe, ce qui le distingue du seul autre pentagone régulier, le pentagramme, qui est étoilé. On peut dessiner un pentagramme régulier en reliant les sommets d'un pentagone régulier par ses diagonales. Les côtés du pentagramme sont parallèles aux côtés du pentagone (utiliser des triangles isocèles et des angles alternes-internes de la figure).

Mesures

Angles

Ils sont indépendants de la taille du pentagone.

• Angle au centre = angle externe : 360/5 = 72°
• Angle interne : 180×(5-2)/5 = 540/5 = 108°, car :
• Somme des angles internes de tout pentagone simple : 180×(5-2) = 540°

Dimensions en fonction du côté

La construction du pentagone régulier à la règle et au compas fait apparaître le nombre d'or représenté par la suite par la lettre grecque φ ("phi")

${\displaystyle \varphi ={{1+{\sqrt {5}}} \over 2}\approx 1,618~034}$

${\displaystyle \varphi =2\cos {\pi \over 5}}$

Quelques caractéristiques^[1] du pentagone régulier convexe de côté a :

• Périmètre :

  ${\displaystyle P=5~a}$

• Aire :

  ${\displaystyle A={\frac {5a^{2}}{4}}\cot {\frac {\pi }{5}}={\frac {a^{2}}{4}}{\sqrt {25+10{\sqrt {5}}}}={\frac {a^{2}}{4}}{\sqrt {15+20\varphi }}\approx 1,720~a^{2}}$

  (cot étant la fonction cotangente)

• Apothème = rayon du cercle inscrit :

  ${\displaystyle r={a \over 2}\cot {\pi \over 5}={a \over 10}{\sqrt {25+10{\sqrt {5}}}}={a \over 10}{\sqrt {15+20\varphi }}\approx 0,688~a}$

• Rayon du cercle circonscrit :

  ${\displaystyle R={a \over {2\sin {\pi \over 5}}}={1 \over 10}{\sqrt {50+10{\sqrt {5}}}}~a={1 \over 5}{\sqrt {10+5\varphi }}~a=\approx 0,851~a}$

• Diagonale (voir à théorème de Ptolémée):

  ${\displaystyle D={\frac {1+{\sqrt {5}}}{2}}~a=\varphi ~a\approx 1,618~a}$

• Hauteur :

  ${\displaystyle H=R+r={1 \over 2}{\sqrt {5+2{\sqrt {5}}}}~a={1 \over 2}{\sqrt {3+4\varphi }}~a\approx 1,539~a}$

• Distance entre un côté et la diagonale parallèle à ce côté :

  ${\displaystyle d_{1}={\sqrt {{5+{\sqrt {5}}} \over 8}}~a={{\sqrt {2+\varphi }} \over 2}~a\approx 0,951~a}$

• Distance entre une diagonale et le sommet le plus proche extérieur à la diagonale :

  ${\displaystyle d_{2}={\sqrt {{5-{\sqrt {5}}} \over 8}}~a={{\sqrt {3-\varphi }} \over 2}~a\approx 0,588~a}$

Dimensions en fonction du rayon du cercle circonscrit

• Côté :

  ${\displaystyle a=2R\sin {\pi \over 5}={\sqrt {{5-{\sqrt {5}}} \over 2}}~R={\sqrt {3-\varphi }}~R\approx 1,176~R}$

• Diagonale :

  ${\displaystyle D={\sqrt {2+\varphi }}~R={\sqrt {\frac {5+{\sqrt {5}}}{2}}}~R\approx 1,902~R}$

• Hauteur :

  ${\displaystyle H=R+r={{5+{\sqrt {5}}} \over 4}~R}$

• Distance entre un côté et la diagonale parallèle à ce côté :

  ${\displaystyle d_{1}={{\sqrt {5}} \over 2}~R\approx 1,118~R}$

• Distance entre une diagonale et le sommet le plus proche extérieur à la diagonale:

  ${\displaystyle d_{2}={{5-{\sqrt {5}}} \over 4}~R\approx 0,691~R}$

Usages

Pavages

Il n'est pas possible de paver le plan euclidien par des pentagones réguliers convexes : la mesure de son angle interne, 108°, n'est pas un diviseur de 360°, la mesure d'un tour complet, ce qui empêche le pentagone de servir de tuile dans un pavage régulier. Il n'est pas possible non plus de paver le plan avec des combinaisons de pentagones et d'autres polygones réguliers et d'obtenir un pavage archimédien, uniforme ou semi-régulier.

• 
  Un carré, un pentagone et un icosagone se rencontrant en un même sommet ; cette configuration ne permet pas de paver le plan.
• 
  Deux pentagones et un décagone réguliers convexes se rencontrant en un même sommet ; cette configuration ne permet pas de paver le plan.
• 
  L'agencement le plus dense connu de pentagones réguliers convexes de même taille sur un plan est une structure couvrant 92,131% de ce plan.

En géométrie hyperbolique, il est possible de paver le plan uniformément par des pentagones réguliers, en faisant se rencontrer au moins 4 pentagones autour de chaque sommet.

• 
  Pavage uniforme du plan hyperbolique par des pentagones, 4 se rencontrant à chaque sommet.
• 
  Pavage hyperbolique, avec 5 pentagones autour de chaque sommet.
• 
  Pavage hyperbolique, avec 6 pentagones autour de chaque sommet.

Polyèdres

Parmi les polyèdres comportant des pentagones réguliers convexes, et de façon non exhaustive :

• Le dodécaèdre régulier, dont les faces sont 12 pentagones réguliers convexes ; il s'agit d'un solide de Platon.
• Le grand dodécaèdre, constitué de 12 faces pentagonales, avec cinq pentagones se rencontrant à chaque sommet, se coupant les uns les autres en créant un trajet pentagrammique ; il s'agit d'un solide de Kepler-Poinsot.
• Parmi les solides d'Archimède : l'icosidodécaèdre, l'icosaèdre tronqué, le petit rhombicosidodécaèdre et le dodécaèdre adouci ; ces polyèdres combinent des faces pentagonales avec d'autres polygones réguliers.
• Le prisme et l'antiprisme pentagonaux

• 
  Dodécaèdre régulier
• 
  Grand dodécaèdre
• 
  Icosidodécaèdre
• 
  Icosaèdre tronqué
• 
  Petit rhombicosidodécaèdre
• 
  Dodécaèdre adouci
• 
  Prisme pentagonal
• 
  Antiprisme pentagonal

Unicode

Référence

Voir aussi

• Portail de la géométrie