Liczba Nusselta

Liczba Nusselta – w termodynamice jedna z liczb podobieństwa. W ośrodku płynnym wyraża ona stosunek szybkości wymiany ciepła w wyniku konwekcji do szybkości wymiany ciepła w wyniku przewodnictwa cieplnego. Liczbę Nusselta definiuje się zwykle jako:

${\displaystyle {\text{Nu}}={\frac {E_{konwekcji}}{E_{przewodzenia}}}={\frac {\alpha \cdot d}{\lambda }},}$

gdzie:

${\displaystyle \alpha }$ – współczynnik wnikania ciepła [W/(m²K)],

${\displaystyle d}$ – charakterystyczny wymiar liniowy [m],

${\displaystyle \lambda }$ – współczynnik przewodzenia ciepła [W/mK].

Jeśli przepływ ciepła w układzie odbywa się wyłącznie poprzez przewodnictwo (konwekcja nie występuje), liczba Nusselta jest równa 1^[1]. Odpowiednikiem liczby Nusselta w procesie wymiany masy jest liczba Sherwooda (Sh).

Wyprowadzenie

Zestawmy przy ściance prawo Newtona dla strumienia ciepła dla konwekcji (lewa strona poniższego równania) i prawa Fouriera dla przewodnictwa (z prawej):

${\displaystyle \alpha (T_{w}-T_{f})=-\lambda \left({\frac {\partial T}{\partial y}}\right)_{w},}$

gdzie: ${\displaystyle \alpha }$ to wsp. wnikania ciepła, ${\displaystyle \lambda }$ to wsp. przewodzenia ciepła, ${\displaystyle T}$ to temperatura, ${\displaystyle T_{w}}$ to temperatura ścianki, ${\displaystyle T_{f}}$ to temperatura płynu w nieskończoności. Pochodna temperatury wzięta w nawias z dolnym indeksem ‘w’ oznacza, że jest liczona, zaczynając od ścianki w kierunku do niej prostopadłym (y). Równanie jest w [W/m²], a więc odzwierciedla natężenie strumienia ciepła.

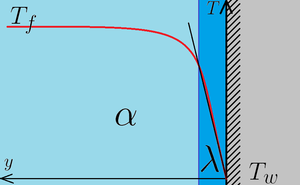
Przy ściance (szary kolor) znajduje się cienka warstwa przyległego (nieruchomego, przylepionego) płynu który przewodzi ciepło (${\displaystyle \lambda ,}$ oraz gradient temperatury od powierzchni ścianki w kierunku płynu), natomiast dalej od ścianki znajduje się ruchomy płyn w którym wymiana ciepła następuje przez konwekcję (${\displaystyle \alpha .}$ ${\displaystyle T_{f}}$ – temperatura płynu w nieskończoności, ${\displaystyle T_{w}}$ – temperatura ścianki). Ilość ciepła przejęta przez przewodzenie musi być równa ilości ciepła przejętego przez przejmowanie. Czerwona linia to temperatura (pionowa oś) względem odległości od ścianki. Naniesiono czarną linię styczną do wykresu temperatury przy ściance, iloczyn jej pochodnej i ${\displaystyle \lambda }$ daje w przybliżeniu natężenie strumienia ciepła związanego z przewodzeniem. Czerwona krzywa obrazuje jak kształtuje się temperatura w zależności od odległości od ścianki (na rysunku założono, że jest chłodniejsza niż płyn w nieskończoności). Po podzieleniu odpowiednim powyższego równania:

${\displaystyle {\frac {\alpha }{\lambda }}=-{\frac {1}{(T_{w}-T_{f})}}\left({\frac {\partial T}{\partial y}}\right)_{w}.}$

Używając dalej teorii podobieństwa, czyli porównując dwa układy: rzeczywisty oraz jego model, otrzyma się liczbę Nusselta następująco:

Układ rzeczywisty	Układ modelowy
${\displaystyle {\frac {\alpha }{\lambda }}=-{\frac {\partial T}{\partial y}}{\frac {1}{T_{w}-T_{f}}}}$	${\displaystyle {\frac {\alpha '}{\lambda '}}=-{\frac {\partial T'}{\partial y'}}{\frac {1}{T_{w}'-T_{f}'}}}$

Definicja stałych podobieństwa ${\displaystyle \alpha {:}}$

${\displaystyle y'=\alpha _{l}y}$	${\displaystyle \alpha '=\alpha _{\alpha }\alpha }$	${\displaystyle T^{'}=\alpha _{T}T}$
	${\displaystyle \lambda '=\alpha _{\lambda }\lambda }$	${\displaystyle t^{'}=\alpha _{t}t}$

Podstawiając te zależności do równania układu modelowego otrzymamy

${\displaystyle {\frac {\alpha _{\alpha }}{\alpha _{\lambda }}}{\frac {\alpha }{\lambda }}=-{\frac {1}{\alpha _{l}}}{\frac {\partial T}{\partial y}}{\frac {1}{T_{w}-T_{f}}}.}$

Z podobieństwa obydwu zjawisk wynika, że równania rzeczywiste i modelowe po podstawieniu zmiennych rzeczywistych, powinny być identyczne. Jest to możliwe w sytuacji, gdy jedno z nich zostało pomnożone przez skalar. Zatem współczynniki zawierające stałe podobieństwa, muszą dawać wartość właśnie tego skalara, zatem muszą być sobie równe tj.:

${\displaystyle {\frac {\alpha _{\alpha }}{\alpha _{\lambda }}}={\frac {1}{\alpha _{l}}},}$

zatem:

Zależność		idem
${\displaystyle {\frac {\alpha _{\alpha }\alpha _{l}}{\alpha _{\lambda }}}=1}$	${\displaystyle \Rightarrow }$	${\displaystyle {\frac {\alpha l}{\lambda }}={\frac {\alpha 'l'}{\lambda '}}=Nu}$

Przykładowa normalizacja

Można znormalizować wejściowe równanie, tak aby otrzymać jego postać bezwymiarową (bez jednostek) dla tego przypadku. Jeżeli dane z obliczeń i różnych eksperymentów zostaną podobnie znormalizowane, to wówczas można je między sobą porównywać. Zatem normalizacja stanowi swego rodzaju wspólny mianownik dla danych pochodzących z różnych źródeł.

Wprowadzając następujące zmienne bezwymiarowe (z gwiazdką)

Zmienna	Jednostka	Zakres zmiennych wymiarowych	Zakres zmiennych bezwymiarowych
${\displaystyle T=T^{*}(T_{w}-T_{f})}$	[K]	${\displaystyle T\in [T_{w},T_{f}]}$	${\displaystyle T^{*}\in [{\frac {T_{w}}{T_{w}-T_{f}}},{\frac {T_{f}}{T_{w}-T_{f}}}]}$
${\displaystyle y=y^{*}L}$	[m]	${\displaystyle y\in [0,L]}$	${\displaystyle y^{*}\in [0,1]}$

gdzie ${\displaystyle L}$ jest wybranym (charakterystycznym) geometrycznym (wymiarowym [m]) – choć równanie generalnie dotyczy obszaru od ścianki w nieskończoność. Jednostką zmiennej ${\displaystyle y}$ jest metr natomiast zmienna ${\displaystyle y^{*}}$ jest bezwymiarowa (nie ma jednostki) – i dopiero iloczyn ${\displaystyle y^{*}L}$ staje się wymiarowy, gdyż parametr ${\displaystyle L}$ zawiera jednostkę [m]. Podobnie rzecz się ma z ${\displaystyle T}$ i ${\displaystyle T^{*}}$ gdzie różnica ${\displaystyle T_{w}-T_{f}}$ zawiera jednostkę [K] podobnie jak zmienna ${\displaystyle T}$ zaś zmienna ${\displaystyle T^{*}}$ nie ma wymiaru.

Do wejściowego równania:

${\displaystyle \alpha (T_{w}-T_{f})=-\lambda \left({\frac {\partial T}{\partial y}}\right)_{w}}$

można podstawić nowe zmienne

${\displaystyle \alpha (T_{w}-T_{f})=-\lambda \left({\frac {\partial (T_{w}-T_{f})T^{*}}{\partial Ly^{*}}}\right)_{w},}$

dostając

${\displaystyle \alpha (T_{w}-T_{f})=-{\frac {(T_{w}-T_{f})}{L}}\lambda \left({\frac {\partial T^{*}}{\partial y^{*}}}\right)_{w},}$

po podzieleniu obustronnym przez ${\displaystyle {\frac {(T_{w}-T_{f})}{L}}\lambda }$ otrzymamy:

${\displaystyle {\frac {\alpha L}{\lambda }}=-\left({\frac {\partial T^{*}}{\partial y^{*}}}\right)_{w},}$

zatem wejściowe równanie przybierze następującą bezwymiarową postać:

${\displaystyle Nu=-\left({\frac {\partial T^{*}}{\partial y^{*}}}\right)_{w}}$

wraz z warunkiem brzegowym (który wynika powyższego podstawienia ${\displaystyle T=T^{*}(T_{w}-T_{f})}$ oraz tego że dla ${\displaystyle y=0}$ ma być ${\displaystyle T=T_{w}}$):

${\displaystyle y=0\Rightarrow T_{w}^{*}=T_{w}/(T_{w}-T_{f}),}$

gdzie liczba Nusselta jest zdefiniowana jako:

${\displaystyle Nu={\frac {\alpha L}{\lambda }}.}$

L to głębokość zbiornika, ${\displaystyle \alpha }$ to wsp. przenikania ciepłą dla wody, ${\displaystyle \lambda }$ to wsp. przewodzenia ciepła dla wody.

Dostając rozwiązanie ${\displaystyle T^{*}}$ (czyli rozkład bezwymiarowej temperatury względem odległości od ścianki w cienkiej nieruchomej warstwie płynu przylegającego do niej) dla tak postawionego bezwymiarowego równania, możemy przeliczyć ten wynik dla układów podobnych (czyli takich które mogą być opisane tym samym równaniem oraz posiadające taką samą wartość liczby Nusselta). Wówczas wynik dla takiego przypadku będzie jako przez ${\displaystyle T=T^{*}(T_{w}-T_{f}).}$

Rozwiązanie dla cienkiej warstwy płynu przylegającego do ścianki, gdzie występują, rozkład temperatury jest liniowy (patrz rysunek powyżej):

Scałkowane obustronnie równanie bezwymiarowe po dy:

${\displaystyle \left.Nu=-\left({\frac {\partial T^{*}}{\partial y^{*}}}\right)_{w}\right/\int dy^{*},}$

dostając:

${\displaystyle T^{*}=C^{*}-y^{*}Nu,}$

gdzie C to stała będąca sumą stałych pojawiających się po lewej i prawej stronie scałkowanego równania.

Uwzględniając warunek brzegowy na ściance (tj. dla ${\displaystyle y^{*}=0}$ jest ${\displaystyle T^{*}(0)=T_{w}^{*}=T_{w}/(T_{w}-T_{f})}$), mamy:

${\displaystyle C=T_{w}^{*}.}$

Zatem rozwiązanie równań bezwymiarowych ma postać:

${\displaystyle T^{*}=T_{w}^{*}-y^{*}Nu.}$

Taka znormalizowana (bezwymiarowa) forma rozwiązania pozwala w łatwy sposób porównywać wyniki między sobą np. dla różnych przypadków zmierzonych eksperymentalnie i podobnie znormalizowanych.

W celu uzyskania wymiaru w rozwiązaniu można odwrócić proces normalizacji wprowadzając ${\displaystyle T^{*}=T/(T_{w}-T_{f}),}$ ${\displaystyle y^{*}=y/L}$ oraz ${\displaystyle Nu={\frac {\alpha L}{\lambda }}}$ i otrzymując:

${\displaystyle T=T_{w}-{\frac {\alpha }{\lambda }}(T_{w}-T_{f})y.}$

Przypisy