Derivasjon

Områder i analyse

Differensialligninger

Funksjonalanalyse

Funksjoner av flere variable

Matematisk analyse

Kontinuitet Grenseverdier Følger Rekker Derivasjon Integrasjon

Komplekse funksjoner

Derivasjon er en operasjon i matematikk der en bestemmer den deriverte av en funksjon. For en funksjon av én reell variabel ${\displaystyle f(x)}$ er den deriverte definert ved

${\displaystyle f\!\,'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}$,

dersom grenseverdien eksisterer. Den deriverte er et mål for endringen i funksjonsverdier ${\displaystyle f(x)}$ når den frie variabelen ${\displaystyle x}$ endres. Geometrisk er den deriverte et uttrykk for stigningstallet til tangenten til funksjonen.

For funksjoner av flere variable kan en definere ulike typer deriverte, som retningsderivert, partiellderivert og totalderivert.

Studiet av derivasjon og differensialer kalles differensialregning. Analysens fundamentalteorem sier at derivasjon og integrasjon er inverse operasjoner, og en bruker derfor ofte betegnelsen differensial- og integralregning. Dette fagfeltet er svært viktig både for matematisk analyse og for anvendt matematikk.

Derivasjon av en reell funksjon av én variabel

En reell funksjon av én variabel er en funksjon ${\displaystyle f:\mathbb {R} \rightarrow \mathbb {R} }$. Et enkelt eksempel er funksjonen som beskriver en rett linje. For en rett linje er stigningstallet lik den deriverte til funksjonen som beskriver linjen.

Stigningstallet for en rett linje

En rett linje kan beskrives med funksjonen

${\displaystyle f(x)=ax+b}$.

Hvis koeffisienten ${\displaystyle b}$ er lik null, så er funksjonen lineær. Koeffisienten ${\displaystyle a}$ er stigningstallet som styrer vinkelen ${\displaystyle \theta }$ som linjen danner med ${\displaystyle x}$-aksen:

${\displaystyle \tan \theta =a}$.

Gitt to punkt ${\displaystyle (x_{1},y_{1})}$ og ${\displaystyle (x_{2},y_{2})}$, så finner en stigningstallet ved

${\displaystyle a={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}$

Symbolet ${\displaystyle \Delta }$ brukes for å beskrive en endring i en størrelse, og ${\displaystyle \Delta x}$ og ${\displaystyle \Delta y}$ er samsvarende endringer:

${\displaystyle \Delta y=f(x+\Delta x)-f(x)}$

Funksjonen som beskriver en rett linje, har derivert ${\displaystyle f'(x)=a}$.

Formell definisjon av den deriverte

En funksjon ${\displaystyle f:U\to \mathbb {R} }$ som avbilder et åpent intervall ${\displaystyle U}$ av reell tall, er deriverbar i ${\displaystyle x_{0}\in U}$ hvis den følgende grenseverdien eksisterer:

${\displaystyle \lim _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}}$   (med ${\displaystyle h=\Delta x=x-x_{0}}$)

Grenseverdien kalles den deriverte til ${\displaystyle f}$ med hensyn på ${\displaystyle x}$ i ${\displaystyle x_{0}}$. Dersom grenseverdien ikke eksisterer, så er funksjonen ikke deriverbar i punktet. Hvis funksjonen er deriverbar i et hvert punkt i intervallet, sies funksjonen å være deriverbar i intervallet. Den deriverte definerer da en ny funksjon i intervallet, ofte skrevet som ${\displaystyle f'(x)}$ eller ${\displaystyle {\frac {df}{dx}}}$:

${\displaystyle f'(x)={\frac {df}{dx}}=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}\qquad x\in U}$.

Ordet «differensierbar» brukes synonymnt med «deriverbar».

Det eksisterer mange ulike skriveformer for funksjonen som er resultat av derivasjonen, drøftet i det følgende avsnittet Notasjon.

En funksjon kan være deriverbar i hele ${\displaystyle \mathbb {R} }$, men kan også ha punkter der den ikke er deriverbar. Det eksisterer funksjoner som ikke er deriverbare i noe punkt, for eksempel funksjonen som beskriver Koch-kurven, navngitt etter Helge von Koch.

Eksempler

Den deriverte til funksjonen ${\displaystyle f(x)=x^{2}-3x+2}$ i punktet ${\displaystyle x=x_{0}}$ kan finnes ved å forenkle differensekvotienten

${\displaystyle {\begin{aligned}{\frac {f(x_{0}+h)-f(x_{0})}{h}}&={\frac {{\bigl (}(x_{0}+h)^{2}-3(x_{0}+h)+2{\bigr )}-(x_{0}^{2}-3x_{0}+2)}{h}}\\&={\frac {x_{0}^{2}+2x_{0}h+h^{2}-3x_{0}-3h+2-x_{0}^{2}+3x_{0}-2}{h}}\\&={\frac {2x_{0}h+h^{2}-3h}{h}}\\&=2x_{0}+h-3.\end{aligned}}}$

Den deriverte finnes ved å ta grenseverdien når ${\displaystyle h\to 0}$:

${\displaystyle f'(x_{0})=\lim _{h\to 0}(2x_{0}+h-3)=2x_{0}-3}$.

Vanligvis finnes den deriverte av en funksjon ved hjelp av regneregler for derivasjon og ikke ved bruk av definisjonen, slik som er gjort her. Regnereglene må imidlertid bevises ved hjelp av definisjonen for den deriverte.

Et eksempel på en funksjon som ikke er deriverbar overalt, er gitt ved absoluttverdi-funksjonen:

${\displaystyle f(x)=|x|=\left\{{\begin{array}{rl}x,&{\text{hvis }}x\geq 0\\-x,&{\text{hvis }}x<0.\end{array}}\right.}$

For ${\displaystyle x\in (-\infty ,0)}$ er den deriverte lik -1, mens i intervallet ${\displaystyle (0,\infty )}$ er den deriverte lik 1. For ${\displaystyle x=0}$ eksisterer de to ensidige grenseverdiene, men da disse ikke er like, så er funksjonen ikke deriverbar for dette argumentet:

${\displaystyle {\begin{alignedat}{2}\lim _{x\nearrow 0}{\frac {f(x)-f(0)}{x-0}}\ &=\ \lim _{x\nearrow 0}{\frac {-x-0}{x-0}}\ &&=\ -1\\[5pt]\lim _{x\searrow 0}{\frac {f(x)-f(0)}{x-0}}\ &=\ \lim _{x\searrow 0}{\frac {x-0}{x-0}}\ &&=\ 1\end{alignedat}}}$.

Et slik punkt hvor den deriverte eksisterer på begge sider, men hvor de ensidige grenseverdiene er ulike, kalles et knekkpunkt for grafen til funksjonen.

Høyere-ordens deriverte

Hvis den deriverte til funksjonen ${\displaystyle f}$ er deriverbar, kan man definere den andrederiverte eller dobbeltderiverte til ${\displaystyle f}$ som den deriverte til den førstederiverte. Denne nye funksjonen kan skrives som ${\displaystyle f''(x)}$. Tilsvarende kan man definere den tredje deriverte ${\displaystyle f'''(x)}$, og så videre.

Den n-te deriverte kalles også den deriverte av orden n.

Ved å bruke samme eksempel som tidligere, finner en

${\displaystyle {\begin{alignedat}{2}f(x)&=x^{2}-3x+2\\f'(x)&=2x-3\\f''(x)&=2\\f'''(x)&=0\end{alignedat}}}$

Geometrisk tolkning

Verdien av den deriverte i et punkt generaliserer stigningskoeffisienten for en rett linje. For en vilkårlig deriverbar funksjon vil verdien av den deriverte være lik stigningskoeffisienten til tangenten til funksjonsgrafen i punktet.

For å definere tangenten starter en med en sekant gjennom to punkt på funksjonsgrafen, ${\displaystyle (x_{0},f(x_{0}))}$ og ${\displaystyle (x_{0}+h,f(x_{0}+h))}$. Ved å la ${\displaystyle h}$ gå mot null, som i grenseverdien som definerer den deriverte, vil sekanten nærme seg tangenten som grense.

Ligningen for tangenten i punktet ${\displaystyle (x_{0},f(x_{0}))}$ er

${\displaystyle y-f(x_{0})=f'(x_{0})(x-x_{0})}$

Den andrederiverte er et mål for krumningen til grafen i et punkt. En rett linje har ingen krumning, og funksjonen har en andrederivert lik null.

Generelt har grafen til en vilkårlig funksjon en krumning ${\displaystyle \kappa }$ gitt ved det følgende uttrykket:^[1]

${\displaystyle \kappa ={f'' \over (1+f'^{2})^{3/2}}}$

Aritmetisk tolkning

Den deriverte til en funksjon ${\displaystyle f}$ i punktet ${\displaystyle x_{0}}$ beskriver den lokale oppførselen til funksjonen i en omegnen om ${\displaystyle x_{0}}$. Fra definisjonen av den deriverte følger det at

${\displaystyle f(x_{0}+h)=f(x_{0})+f'(x_{0})h+r(x,h)}$

Leddet ${\displaystyle r(x_{0},h)}$ er en funksjon av både ${\displaystyle x_{0}}$ og ${\displaystyle h}$, og leddet må gå mot null når ${\displaystyle h}$ går mot null. For en liten verdi av ${\displaystyle h}$ kan en derfor bruke tilnærmingen

${\displaystyle f(x_{0}+h)\approx f(x_{0})+f'(x_{0})h}$

Den deriverte er et mål på den lineære andelen av endringen i ${\displaystyle f(x)}$, når ${\displaystyle x}$ endres med et vilkårlig lite tall. En slik vilkårlig liten endring kalles en infinitesimal endring. Når tilnærmingen brukes for en endelig verdi av ${\displaystyle h}$, omtales tilnærmingen som en linearisering av funksjonen.

Antideriverte

Antiderivasjon er prosessen for å finne en antideriverte funksjon, også kalt en primitiv funksjon. En funksjon ${\displaystyle F(x)}$ er en primitiv funksjon til ${\displaystyle f(x)}$ dersom funksjonen ${\displaystyle f}$ er dens deriverte, det vil si dersom ${\displaystyle F'(x)=f(x)}$.

Notasjon for deriverte

Det eksisterer flere forskjellige skriveformer for deriverte, brukt både gjennom historisk tid og i dag.

Leibniz' notasion

Symbolene ${\displaystyle dx}$, ${\displaystyle dy}$ og ${\displaystyle {\frac {dy}{dx}}}$ ble introdusert av Gottfried Leibniz i 1675.^[2] Denne skrivemåten er fremdeles vanlig brukt når en ønsker å understreke funksjonssammenhengen ${\displaystyle y=f(x)}$. Den første-ordens deriverte skrives som en infinitesimal brøk

${\displaystyle {\frac {dy}{dx}},\quad {\frac {df}{dx}},{\text{ eller }}{\frac {d}{dx}}f}$.

Høyere-ordens deriverte av orden n uttrykkes på formen

${\displaystyle {\frac {d^{n}y}{dx^{n}}},\quad {\frac {d^{n}f}{dx^{n}}}{\text{ eller }}{\frac {d^{n}}{dx^{n}}}f}$

Den deriverte for et gitt argument ${\displaystyle x=x_{0}}$ kan med denne notasjonen skrives som

${\displaystyle \left.{\frac {dy}{dx}}\right|_{x=x_{0}}={\frac {dy}{dx}}(x_{0}).}$

Lagranges notasjon

En svært vanlig form for symbol for den deriverte stammer fra Joseph Louis Lagrange og bruker et primtegn sammen med symbolet for funksjonen. Notasjonen ble første gang brukt i verket Theorie des fonctions analytiques i 1797.^[3] Den deriverte av funksjonen ${\displaystyle f}$ symboliseres med${\displaystyle f'}$. Høyere-ordens deriverte kan skrives ved å gjenta primtegnet, slik at den andre-deriverte er ${\displaystyle f''}$. For deriverte av orden høyere enn tre, kan en sette ordenstallet med opphøyd skrift, enten med romertall eller med vanlige tallsymbol:

${\displaystyle f^{\mathrm {iv} }}$   eller   ${\displaystyle f^{(4)}.}$

Lagranges notasjon er mer praktisk enn Leibniz' når en vil understreke at den deriverte er en selvstendig funksjon.

Newtons notasjon

Newtons notasjon for å symbolisere tidsderiverte går tilbake til 1665.^[4] Bruk av denne notasjonen finnes vanlig både i fysikk og matematikk. For en funksjon der argumentet representerer tid, kan en prikk over funksjonen symbolisere derivasjon. Hvis ${\displaystyle y=f(t)}$, så representerer de følgende funksjonene den førstederiverte og den andrederiverte:

${\displaystyle {\dot {y}}\qquad \qquad {\ddot {y}}}$.

Prikk-notasjonen er også brukt i differensialgeometri for den deriverte med hensyn på buelengden.^[5]

Eulers notasjon

Leonhard Euler forsvarte i 1755 notasjonen ${\displaystyle df}$ for den deriverte funksjonen, men dette skapte en del forvirring jevnført med Leibniz' skrivemåte.^[6] I 1800 foreslo Louis François Antoine Arbogast i steden å bruke en stor bokstav ${\displaystyle D}$ for en differensialoperator som operert på funksjonen ${\displaystyle f}$ gir den første-deriverte ${\displaystyle Df}$.^[7] Den n-te deriverte skrives ${\displaystyle D^{n}f}$. For å presisere hva som er den uavhengige variabelen, så kan denne skrives med nedfelt skrift: Hvis funksjonen er ${\displaystyle y=f(x)}$, så skrives da den deriverte som

${\displaystyle D_{x}y}$   eller   ${\displaystyle D_{x}f(x)}$.

Utregning av den deriverte

Den deriverte til en gitt funksjon regnes vanligvis ut ved å kombinere

• kjennskap til deriverte for et sett av elementære funksjoner; med
• et sett av derivasjonsregler for å behandle sammensatte funksjoner.

Derivasjon av elementære funksjoner

Konstante funksjoner

${\displaystyle {\frac {d}{dx}}a=0}$

Potensfunksjonen

${\displaystyle {\frac {d}{dx}}x^{a}=ax^{a-1}.}$

Eksponential- og logaritmefunksjoner

${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}.}$

${\displaystyle {\frac {d}{dx}}a^{x}=a^{x}\ln(a),\qquad a>0}$

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}},\qquad x>0.}$

${\displaystyle {\frac {d}{dx}}\log _{a}(x)={\frac {1}{x\ln(a)}},\qquad x,a>0}$

Trigonometriske funksjoner

${\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x).}$

${\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x).}$

${\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).}$

Inverse trigonometriske funksjoner

${\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}$

${\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}$

${\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}$

Derivasjonsregler

La ${\displaystyle f}$, ${\displaystyle g}$ og ${\displaystyle h}$ være reelle, deriverbare funksjoner. La videre ${\displaystyle n}$ og ${\displaystyle a}$ være reelle tall. Da gjelder:

Faktorregelen

${\displaystyle (a\cdot f)'=a\cdot f'}$

Summeregelen

${\displaystyle \left(g\pm h\right)'=g'\pm h'}$

Produktregelen

${\displaystyle (g\cdot h)'=g'\cdot h+g\cdot h'}$

Kvotientregelen eller brøkregelen

${\displaystyle \left({\frac {g}{h}}\right)'={\frac {g'\cdot h-g\cdot h'}{h^{2}}}}$

Kjerneregelen

${\displaystyle (g\circ h)'(x)=(g(h(x)))'=g'(h(x))\cdot h'(x)}$

Kombinert kjerne og produktregel

${\displaystyle {\begin{alignedat}{2}f&=c\cdot k^{u}\cdot l^{v}\cdot m^{w}\cdot ...\\[5pt]f'&=f\cdot ({\frac {u}{k}}\cdot k'+{\frac {v}{l}}\cdot l'+{\frac {w}{m}}\cdot m'+...)\end{alignedat}}}$

Inverse funksjoner

Hvis ${\displaystyle f}$ er en bijektiv funksjon som er deriverbar i ${\displaystyle x_{0}}$ med ${\displaystyle f'(x_{0})\neq 0}$, og den inverse funksjonen ${\displaystyle f^{-1}}$ er deriverbar ved ${\displaystyle f(x_{0})}$, så gjelder:

${\displaystyle (f^{-1})'(f(x_{0}))={\frac {1}{f'(x_{0})}}.}$

Leibniz’ regel

${\displaystyle (fg)^{(n)}=\sum _{k=0}^{n}{n \choose k}f^{(k)}g^{(n-k)}}$.

Her er ${\displaystyle {n \choose k}}$ binomialkoeffisienter.

Implisitt derivasjon

Hvis en funksjon ${\displaystyle y=y(x)}$ er definert implisitt ved en ligning

${\displaystyle F\left(x,y(x)\right)=0}$,

så følger det av den generaliserte kjerneregelen for funksjoner av flere variabler at

${\displaystyle F_{x}+F_{y}y'=0.}$

I denne ligningen er

${\displaystyle {\begin{alignedat}{2}F_{x}={\frac {\partial F}{\partial x}}\\F_{y}={\frac {\partial F}{\partial y}}\end{alignedat}}}$

partiell deriverte av funksjonen ${\displaystyle F}$. Forutsatt at den partiell deriverte ${\displaystyle F_{y}}$ er ulik null, så kan den deriverte av funksjonen ${\displaystyle y=y(x)}$ uttrykkes som en brøk:

${\displaystyle y'=-{\frac {F_{x}}{F_{y}}}}$

Eksempel

Gitt funksjonen

${\displaystyle f(x)=x^{4}+\sin \left(x^{2}\right)-\ln(x)e^{x}+7}$

Den deriverte er da gitt som følger:

${\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {d\left(x^{2}\right)}{dx}}\cos \left(x^{2}\right)-{\frac {d\left(\ln {x}\right)}{dx}}e^{x}-\ln(x){\frac {d\left(e^{x}\right)}{dx}}+0\\&=4x^{3}+2x\cos \left(x^{2}\right)-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}$

Det første leddet er derivert ved å bruke regelen for en potensfunksjon. Det andre leddet er håndtert ved hjelp av kjerneregelen samt regler for derivasjon av trigonometriske funksjoner og potensfunksjoner. Derivasjon av det tredje leddet er gjennomført ved å bruke produktregelen.

Egenskaper til deriverbare funksjoner

Derivasjon og kontinuitet

En funksjon som er deriverbar for ${\displaystyle x=x_{0}}$, er også kontinuerlig i ${\displaystyle x=x_{0}}$. En funksjon kan altså ikke være deriverbar i en diskontinuitet.

Omvendt kan en funksjon være kontinuerlig i et punkt, uten å være deriverbar i punktet. Et eksempel på dette er punktet ${\displaystyle x=0}$ for absoluttverdi-funksjonen.

Dersom funksjonen har en derivert som også er kontinuerlig, sies funksjonen å være kontinuerlig deriverbar. Hvis den n-te ordens deriverte eksisterer og er kontinuerlig, så er funksjonen n ganger kontinuerlig deriverbar. Klassen av slike funksjoner er viktig nok til å ha fått sitt eget symbol:

${\displaystyle C^{n}(D)}$

betegner klassen av funksjoner som er n ganger kontinuerlig deriverbar på definisjonsmengden ${\displaystyle D}$. Klassen av kontinuerlige funksjoner er ${\displaystyle C^{0}}$. En funksjon som er uendelig mange ganger kontinuerlig deriverbar kalles en glatt funksjon, og klassen av slike funksjoner betegnes som ${\displaystyle C^{\infty }}$.

Generelt gjelder at

${\displaystyle C^{n}\subset C^{n-1}\subset \dots \ C^{1}\subset C^{0}}$.

Middelverdisetningen

For en funksjon som er deriverbar i et intervall, vil stigningen til sekanten mellom to vilkårlige punkt på grafen til funksjonen være et uttrykk for den midlere endringen til funksjonen mellom de to punktene. Middelverdisetningen uttrykker at grafen til funksjonen mellom de to punktene må ha en tangent med samme stigning som sekanten. Setningen kalles også sekantsetningen:

La ${\displaystyle f:[a,b]\to \mathbb {R} }$ være en funksjon som er kontinuerlig på et lukket intervall ${\displaystyle [a,b]}$ (med ${\displaystyle a<b}$). Anta videre at ${\displaystyle f}$ er deriverbar i det åpne intervallet ${\displaystyle (a,b)}$. Da finnes minst ett punkt ${\displaystyle x_{0}\in (a,b)}$, slik at

${\displaystyle f'(x_{0})={\frac {f(b)-f(a)}{b-a}}}$.

Dersom ${\displaystyle f(a)=f(b)}$, medfører dette at funksjonen må ha en derivert mellom ${\displaystyle a}$ og ${\displaystyle b}$ som er lik null, det vil si at tangenten er horisontal. Dette spesialtilfellet av middelverdisetningen kalles Rolles sats.

Monotonisitet

En funksjon er monoton i et intervall dersom den er voksende eller minkende i hele intervallet. Tilsvarende sier en også at funksjonen er strengt monoton i et intervall dersom den er strengt voksende eller strengt minkende i hele intervallet. Disse egenskapene følger direkte fra middelverdisetningen.

En deriverbar funksjon er voksende i et intervall dersom den deriverte av funksjonen er ikke-negativ i hele intervallet. Tilsvarende er funksjonen minkende i et intervall dersom den deriverte er ikke-positiv i intervallet.

En deriverbar funksjon er strengt voksende i et intervall dersom den deriverte av funksjonen er positiv i hele intervallet. Tilsvarende er funksjonen strengt minkende i et intervall dersom den deriverte er negativ i intervallet.

Ekstremalverdier og vendepunkt

Dersom en funksjon er deriverbar i et punkt ${\displaystyle x=x_{0}}$, så er ${\displaystyle f'(x_{0})=0}$ et nødvendig vilkår for at funksjonen skal ha et ekstremalpunkt for dette argumentet. Et punkt der den deriverte er lik null kalles et stasjonært punkt.^[8] Sammen med punkt der funksjonen ikke er deriverbar og eventuelle endepunkt for et definisjonsintervall, kalles dette også kritiske punkt. Et ekstremalpunkt må alltid være et kritisk punkt.^[9] Et terassepunkt er et stasjonært punkt der den deriverte ikke skifter fortegn.^[10]

For et punkt ${\displaystyle x=x_{0}}$ der en funksjon er deriverbar vil hver av de to følgende testene gi tilstrekkelige vilkår for at punktet er et maksimumspunkt:

• ${\displaystyle x=x_{0}}$ er et lokalt strengt maksimumspunkt dersom ${\displaystyle f'(x_{0})=0}$ og den deriverte skifter fortegn fra positiv til negativ når ${\displaystyle x}$ vokser gjennom ${\displaystyle x_{0}}$.

• ${\displaystyle x=x_{0}}$ er et lokalt strengt maksimumspunkt dersom ${\displaystyle f'(x_{0})=0}$ og ${\displaystyle f''(x_{0})<0}$.

Tilsvarende har en for et minimumspunkt:

• ${\displaystyle x=x_{0}}$ er et lokalt strengt minimumspunkt dersom ${\displaystyle f'(x_{0})=0}$ og den deriverte skifter fortegn fra negativ til positiv når ${\displaystyle x}$ vokser gjennom ${\displaystyle x_{0}}$.

• ${\displaystyle x=x_{0}}$ er et lokalt strengt minimumspunkt dersom ${\displaystyle f'(x_{0})=0}$ og ${\displaystyle f''(x_{0})>0}$.

Kartlegging av ekstremalpunkt inngår som en viktig del av funksjonsdrøfting.

Krumning og vendepunkt

En funksjon er konveks i et intervall dersom en rett linje mellom to vilkårlige punkt i intervallet ligger over grafen til funksjonen i intervallet. Dette kan også uttrykkes som at grafen til funksjonen vender den hule siden oppover eller krummer opp. Funksjonen er strengt konveks dersom grafen ligger helt under den rette linjen. Tilsvarende kan en definere at funksjonen er konkav, dersom den vender den hule siden nedover eller krummer ned.

En deriverbar funksjon er konveks eller krummer opp i et intervall dersom den deriverte er voksende i intervallet. En funksjon som er to ganger deriverbar, er strengt konveks i et intervall dersom den dobbelt-deriverte ${\displaystyle f''(x)}$ er positiv i intervallet. Den dobbelt-deriverte kan også være lik null i isolerte punkt i intervallet.

Funksjonen ${\displaystyle f(x)=x^{4}}$ har dobbelt-derivert ${\displaystyle f''(x)=12x^{2}}$. Funksjonen er altså strengt konveks i hele ${\displaystyle \mathbb {R} }$.

I differensialgeometri er krumningen ${\displaystyle \kappa }$ til en funksjon gitt ved det følgende uttrykket:^[11]

${\displaystyle \kappa ={f'' \over (1+f'^{2})^{3/2}}}$

Et vendepunkt er et stasjonært punkt ${\displaystyle x_{0}}$ der funksjonen skifter krumning, fra opp til ned eller omvendt. Dette vil være tilfelle dersom den dobbelt-deriverte skifter fortegn i punktet.

Funksjonen ${\displaystyle f(x)=x^{3}}$ har dobbelt-derivert ${\displaystyle f''(x)=6x}$. Funksjonen har altså et vendepunkt i ${\displaystyle x=0}$.

Taylorrekker

Taylors teorem sier at en funksjon som er (${\displaystyle n+1}$) ganger kontinuerlig deriverbar på et intervall ${\displaystyle I}$, kan tilnærmes med et polynom i intervallet, og teoremet gir også et uttrykk for feilen i denne tilnærmingen. Dersom ${\displaystyle x=a}$ er et vilkårlig punkt i intervallet, så er

${\displaystyle f(x)=T_{n}(x;a)+R_{n+1}(x;a)\qquad \forall x\in I}$

Her er ${\displaystyle T_{n}}$ taylorpolynomet av grad ${\displaystyle n}$:

${\displaystyle {\begin{aligned}T_{n}(x;a)&=\sum _{k=0}^{n}\left({\frac {f^{(k)}(a)}{k!}}(x-a)^{k}\right)\\&=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\end{aligned}}}$.

Restleddet ${\displaystyle R_{n+1}}$ kan uttrykkes på flere forskjellige måter, og Joseph Louis Lagranges form er gitt som^[12]

${\displaystyle R_{n+1}(x;a)={\frac {1}{(n+1)!}}f^{(n+1)}(b)(x-a)^{n+1}\qquad }$.

Argumentet ${\displaystyle b}$ er en verdi mellom ${\displaystyle x}$ og ${\displaystyle a}$. Når ${\displaystyle n=1}$ svarer Taylors formel til middelverdisetningen.

I mange praktske anvendelser brukes tilnærmingen ${\displaystyle f(x)=T_{n}(x;a)}$, og restleddet er da et uttrykk for feilen i tilnærmingen. Feilen vil typisk vokse når ${\displaystyle x}$ fjerner seg fra verdien ${\displaystyle a}$.

For en glatt funksjon kan en i noen tilfeller vise at funksjonen kan uttrykkes som en uendelig konvergent taylorrekke:

${\displaystyle {\begin{aligned}f(x)&=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+\dotsb \\&=\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.\end{aligned}}}$

Denne sammenhengen gjelder imidlertid ikke for alle glatte funksjoner. En glatt funksjon som samsvarer lokalt med sin egen taylorrekke, kalles en analytisk funksjon.^[13]

Analysens fundamentalteorem

Analysens fundamentalteorem uttrykker en sammenheng mellom derivasjon og integrasjon.^[14]

Hvis ${\displaystyle f:[a,b]\to \mathbb {R} }$ er en integrerbar funksjon, så er funksjonen

${\displaystyle F(x)=\int _{a}^{x}f(t)\,\mathrm {d} t\qquad x\in [a,b]}$

kontinuerlig i intervallet ${\displaystyle [a,b]}$. Hvis ${\displaystyle f}$ er deriverbar i ${\displaystyle x=x_{0}}$, så er også ${\displaystyle F}$ deriverbar i dette punktet, og ${\displaystyle F\,'(x_{0})=f(x_{0})}$.

Teoremet gir en bruksanvisning for kunne integrere en funksjon ${\displaystyle f}$, omtalt som integranden. Dersom den antideriverte til integranden kan bestemmes som ${\displaystyle F}$, så er

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a)}$.

Derivasjon av en kompleks funksjon av én variabel

Formell definisjon

Definisjonen av en kompleks funksjon ${\displaystyle f:\mathbb {C} \rightarrow \mathbb {C} }$ er i notasjon lik definisjonen for en reell funksjon:

${\displaystyle f\!\,'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}$.

Forskjellen ligger i definisjonen av grenseverdien, som nå er definert i det komplekse planet. Den komplekse størrelsen ${\displaystyle h}$ skal nå kunne nærme seg null langs en vilkårlig rute i det kompekse planet. Dette gjør at definisjonen av deriverbarhet for komplekse funksjoner er et strengere krav enn deriverbarhet for reelle funksjoner. Realdelen og imaginærdelen av en kompleks funksjon kan hver for seg være deriverbare, uten at den komplekse funksjonen er deriverbar.

En kompleks funksjon kan være deriverbar i et punkt, uten å være deriverbar i andre nærliggende punkt. En kompleks funksjon sies å være en analytisk funksjon i et punkt dersom funksjonen er deriverbar i en omegn om punktet. Begrepet holomorf funksjon er synonymt med analytisk funksjon. En funksjon som er analytisk i hele det komplekse planet, kalles en hel funksjon.

Cauchy-Riemann-ligningene

En kompleks funksjon kan generelt skrives på formen

${\displaystyle f(z)=u(x,y)+iv(x,y)\qquad \qquad z=x+iy}$

der ${\displaystyle i}$ er den imaginære enheten, med egenskapen ${\displaystyle i^{2}=-1}$. De to funksjonene ${\displaystyle u}$ og ${\displaystyle v}$ er reelle funksjoner. Hvis funksjonen ${\displaystyle f(z)}$ er deriverbar, så er også de to Cauchy-Riemann-ligningene oppfylte. Dette er to differensialligninger på formen

${\displaystyle {\begin{alignedat}{2}u_{x}&=v_{y}\\u_{y}&=-v_{x}\end{alignedat}}}$

Ligningene er oppkalt etter Augustin Louis Cauchy og Bernhard Riemann. Den deriverte er gitt ved

${\displaystyle f'(z)=u_{x}+iv_{x}=v_{y}-iv_{x}}$

Omvendt gjelder at dersom de to funksjonene ${\displaystyle u}$ og ${\displaystyle v}$ har kontinuerlige deriverte med hensyn på begge variablene, og de deriverte oppfyller Cauchy-Riemann-ligningene, så er funksjonen ${\displaystyle f}$ deriverbar.

Eksempler

Den komplekse eksponentialfunksjonen kan defineres ved

${\displaystyle f(z)=e^{z}=e^{x}(\cos y+i\sin y)\qquad \qquad z=x+iy}$

De to funksjonene

${\displaystyle {\begin{alignedat}{2}u(x,y)=e^{x}\cos y\\v(x,y)=e^{x}\sin x\end{alignedat}}}$

har begge kontinuerlige deriverte og oppfyller Cauchy-Riemann-ligningene. Da følger det at

${\displaystyle f'(z)=u_{x}+iv_{x}=e^{x}(\cos y+i\sin y)=e^{z}}$

Også den komplekse eksponentialfunksjonen er lik sin egen derivert. Eksponentialfunksjonen er en hel funksjon. Siden de trigonometriske funksjonene ${\displaystyle \sin z}$ og ${\displaystyle \cos z}$ kan defineres som lineærkombinasjonar av den komplekse eksponentialfunksjonen, er også disse to funksjonene hele. Alle polynomfunksjoner er hele funksjoner.

Den komplekse funksjonen ${\displaystyle f(z)=|z|^{2}}$ er deriverbar kun for argumentet ${\displaystyle z=0}$.

Generalisering til andre typer funksjoner

Flere typer deriverte kan defineres for funksjoner, også for funksjonstyper der argumentet ikke er et reelt eller et komplekst tall.

Retningsderivasjon for skalarfelt

Et skalarfelt er en reell funksjon av flere variable, på formen

${\displaystyle y=f({\mathbf {x} }):D\rightarrow \mathbb {R} \qquad D\subset \mathbb {R} ^{n}}$

Argumentet ${\displaystyle {\mathbf {x} }=(x_{1},x_{2},x_{3},...,x_{n})}$ er her en n-dimensjonal vektor.

For et skalarfelt kan en definere den retningsderiverte i retningen ${\displaystyle {\mathbf {v} }\in \mathbb {R} ^{n}}$ ved^[15]

${\displaystyle f'({\mathbf {x} };{\mathbf {v} })=\lim _{h\to 0}{\frac {f({\mathbf {x} }+h{\mathbf {v} })-f({\mathbf {x} })}{h}}}$

forutsatt at grenseverdien eksisterer. Det er ikke krav at vektoren ${\displaystyle {\mathbf {v} }}$ skal ha lengde lik én. Eksistens av en retningsderivert er ikke tilstrekkelig for at funksjonen skal være kontinuerlig.

Den retningsderiverte oppfyller et middelverditeorem, tilsvarende en funksjon av én variabel: Dersom den retningsderiverte ${\displaystyle f'({\mathbf {x} +t{\mathbf {v} }};{\mathbf {v} })}$ eksisterer for alle verdier av ${\displaystyle t}$ i intervallet ${\displaystyle [0,1]}$, så er

${\displaystyle f({\mathbf {x} }+{\mathbf {v} })-f({\mathbf {x} })=f'({\mathbf {x} +\theta {\mathbf {v} }};{\mathbf {v} })\qquad \theta \in (0,1)}$

Partiell derivasjon

For et skalarfelt er den partiellderiverte det samme som den retningsderivert langs en av akseretningene, gitt at retningsvektoren har lengde én. Vanligvis uttrykkes definisjonen av den partiellderiverte med hensyn på variabelen ${\displaystyle x_{i}}$ på formen

${\displaystyle {\frac {\partial f}{\partial x_{i}}}=\lim _{h\to 0}{\frac {f(x_{1},\dots ,x_{i}+h,\dots ,x_{n})-f(x_{1},\dots ,x_{i},\dots ,x_{n})}{h}}}$,

forutstatt at grenseverdien eksisterer. Et skalarfelt med definisjonsmengde i ${\displaystyle \mathbb {R} ^{n}}$ kan ha ${\displaystyle n}$ partiellderiverte.

For en funksjon ${\displaystyle f=f(x,y,z)}$ kan en bruke flere typer notasjon for partiellderiverte:

${\displaystyle {\begin{alignedat}{2}{\frac {\partial f}{\partial x}}=f_{x}=D_{x}f\\{\frac {\partial f}{\partial y}}=f_{y}=D_{y}f\\{\frac {\partial f}{\partial z}}=f_{z}=D_{z}f\\\end{alignedat}}}$

De partiellderiverte uttrykker endringene i funksjonen i hver av retningene parallelt med aksene. Dersom ${\displaystyle f=f(x,y,z)}$ representerer variasjonen i temperatur i et rom, så er ${\displaystyle f_{x}}$ et mål for temperaturendringen i ${\displaystyle x}$-retningen.

Gradienten til en funksjon er en vektor sammensatt av alle partiellderiverte. For ${\displaystyle f=f(x,y,z)}$ uttrykkes gradienten som

${\displaystyle \nabla f=(f_{x},f_{y},f_{z})}$

Denne vektoren vil peke i retningen der funksjonen endrer seg mest. Dersom gradienten er definert, så er den retningsderiverte i retningen ${\displaystyle {\mathbf {v} }}$ gitt ved

${\displaystyle f'({\mathbf {x} };{\mathbf {v} })={\mathbf {v} }\cdot \nabla f}$

Også for partiellderiverte kan en definere høyere-ordens deriverte, i alle kombinasjoner, for eksempel

${\displaystyle {\begin{alignedat}{2}{\frac {\partial ^{2}f}{\partial x^{2}}}=f_{xx}\\{\frac {\partial ^{2}f}{\partial x\partial y}}=f_{xy}\end{alignedat}}}$

Hessematrisen er en matrise av alle de andre-ordens partiell deriverte til et skalarfelt. Ekstremalverdier for et skalarfelt kan studeres ved hjelp av gradienten og hessematrisen.

Et tilstrekkelig vilkår for at de to partiell deriverte ${\displaystyle f_{xy}}$ og ${\displaystyle f_{yx}}$ skal være like i et punkt, er at begge eksisterer og er kontinuerlige i punktet.^[16]

Derivasjon for vektorfelt

Et vektorfelt er en funksjon der både argument og funksjonsverdi er vektorer:

${\displaystyle {\begin{alignedat}{2}{\mathbf {y} }&={\mathbf {f} }({\mathbf {x} }):D\rightarrow \mathbb {R} ^{m}\qquad D\subset \mathbb {R} ^{n}\\{\mathbf {x} }&=(x_{1},x_{2},x_{3},.....,x_{n})\\{\mathbf {y} }&=(y_{1},y_{2},y_{3},...,y_{m})\end{alignedat}}}$

For hver av komponentene i funksjonsverdien kan en definere partiellderiverte:

${\displaystyle {\frac {\partial f_{i}}{\partial x_{j}}}}$

Jacobimatrisen til et vektorfelt er en ${\displaystyle (m\times n)}$-matrise der elementene er første-ordens partiellderiverte:

${\displaystyle {\mathbf {J} }={\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{1}}{\partial x_{n}}}\\\vdots &\ddots &\vdots \\{\dfrac {\partial f_{m}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{m}}{\partial x_{n}}}\end{bmatrix}}}$

For vektorfelt kan en også definere total derivasjon.

Total derivasjon

Den totalderiverte til et generelt vektorfelt er en transformasjon som lokalt er den beste lineære tilnærmingen til funksjonen.

En funksjon ${\displaystyle f:U\to V}$, hvor ${\displaystyle U}$ er en åpen mengde i ${\displaystyle \mathbb {R} ^{n}}$ kalles totalt deriverbar eller totalderiverbar i punktet ${\displaystyle x_{0}\in U}$, hvis det finnes en lineær avbildning ${\displaystyle L:\,\mathbb {R} ^{n}\to \mathbb {R} ^{m}}$ slik at

${\displaystyle \lim _{h\to 0}{\frac {\|f(x_{0}+h)-f(x_{0})-Lh\|}{\|h\|}}=0}$.

Hvis en slik lineær avbildning ${\displaystyle L}$ eksisterer, er den entydig bestemt og avhenger ikke av hvilken norm som benyttes.

For ${\displaystyle n=m=1}$ svarer den totalderiverte til den ordinære deriverte av en reell funksjon. For et skalarfelt er ${\displaystyle m=1}$, og den totalderiverte er lik gradienten til funksjonen. For et vektorfelt er jacobimatrisen en representasjon av den lineære transformasjonen.

En funksjon som er totalderiverbar i et punkt, vil være kontinuerlig i punktet.

Hvis den totalderiverte eksisterer i et punkt, så eksisterer også alle de partiellderiverte i punktet. Omvendt vil ikke eksistensen til samtlige partiell deriverte i et punkt ${\displaystyle x_{0}}$ garantere at den totalt deriverte eksisterer i punktet. Er de partiellderiverte definert og kontinuerlige i en omegn om ${\displaystyle x_{0}}$, så er funksjonen totalderiverbar i ${\displaystyle x_{0}}$.

Anvendelser

Beskrivelse av endringer

Derivasjon blir brukt i mange matematiske modeller der en må beskrive endringer av en eller annen type. Typisk vil en endring av en størrelse ${\displaystyle f}$ over tid kunne uttrykkes som den deriverte ${\displaystyle f'}$ eller en partiell derivert ${\displaystyle f_{t}}$. En endring i størrelsen i rommet kan tilsvarende beskrives som en partiell derivert med hensyn på en romlig koordinat eller en gradient.

Den førstederiverte til en strekning ${\displaystyle s=s(t)}$ etter tiden ${\displaystyle t}$ representerer en skalar hastighet, mens den andrederiverte er et uttrykk for akselerasjonen. I det tredimensjonale rommet er den deriverte a posisjonsvektoren ${\displaystyle \mathbf {r} =\mathbf {r} (t)}$ lik den vektorielle hastigheten.

Vinkelhastigheten er definert som den tidsderiverte av en rotasjonsvinkel, og vinkelakselerasjonen er den andrederiverte.

Differensialligninger

En differensialligning er en ligning som kombinerer deriverte av en funksjon med funksjonen selv samt koeffisienter der den uavhengige variabelen inngår. Et eksempel er differensialligningen

${\displaystyle y''-y=0}$

Den ukjente i en differensialligning er en funksjon. Ligningen over har løsningen

${\displaystyle y=Ae^{x}+Be^{-1}}$,

der ${\displaystyle A}$ og ${\displaystyle B}$ er vilkårlige konstanter.

Dersom den ukjente er en funksjon av én variabel, sies ligningen å være en ordinær differensialligning. En partiell differensialligning inneholder partiellderiverte, og den ukjente er en funksjon av flere variable.

Newtons bevegelseslov kan gi opphav til mange differensialligninger. Loven kombinerer kraft ${\displaystyle \mathbf {F} }$, masse ${\displaystyle m}$ og akselerasjon ${\displaystyle \mathbf {a} }$:

${\displaystyle \mathbf {F} (t)=m\mathbf {a} (t)=m{\ddot {\mathbf {r} }}=m{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}}$

Dersom kraften for eksempel kan uttrykkes som en funksjon av posisjonen ${\displaystyle {\mathbf {r} }}$, så leder dette til en differensialligning for posisjonen.

Et eksempel fra økonomi

I mikroøkonomi kan en analysere forskjellige former for produksjonsfunksjoner, for å skape forståelse for makroøkonomiske sammenhenger. Det er først og fremst den typiske oppførselen til en produksjonsfunksjon som er av interesse: Hvordan reagerer de avhengige variablene ${\displaystyle y}$ (for eksempel den mengden av en vare som produseres) når ${\displaystyle x}$ (for eksempel arbeid eller kapital) økes med en (infinitesimal) enhet.

En grunntype av produksjonsfunksjoner er den nyklassiske produksjonsfunksjonen. Denne funksjonen har egenskapen at produksjonen stiger når argumentet øker, samtidig som at økningen avtar når argumentet vokser. For eksempel kan man ha den følgende produksjonsfunksjonen for en virksomhet:

${\displaystyle y=f(x)={\sqrt {4x-400}}\quad \mathrm {for} \quad x\geq 100}$

Den deriverte følger av kjerneregelen:

${\displaystyle f'(x)={\frac {2}{\sqrt {4x-400}}}}$.

Da rotuttrykket alltid er positivt, vil produksjonen øke med økende innverdi. Den andrederiverte er gitt ved

${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}=-{\frac {4}{\sqrt {(4x-400)^{3}}}}}$.

Denne er alltid negativ, så økningen er synkende.

Historie

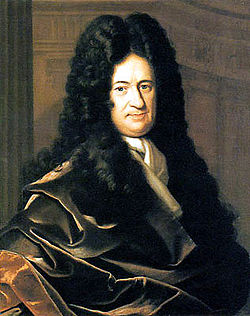
Problemstillingen som differensialregningen betrakter, var kjent som tangentproblemet helt siden antikken. Den nærliggende løsningen var å approksimere tangenten ved hjelp av sekanter over et positivt, men vilkårlig lite intervall. Den tekniske vanskeligheten bestod av å regne med slike infinitesimalt små intervallengder. Pierre de Fermat løste rundt 1640 tangentproblemer for polynomer. Her beskrev han den deriverte, men uten å betrakte grenseverdier, og uten å forklare hva den matematiske rettferdiggjøringen for fremgangsmåten hans var. På samme tid valgte Descartes en algebraisk fremgangsmåte, hvor han anbrakte en sirkel nær kurven. Her vil sirkelen skjære kurven i to punkter, med mindre sirkelen og kurven tangerer hverandre. Da var det mulig å bestemme stigningen til tangenten for visse kurver.

På slutten av 1600-tallet lyktes det Isaac Newton og Gottfried Wilhelm Leibniz uavhengig av hverandre å utvikle fungerende fremgangsmåter uten selvmotsigelser. Newton og Leibniz angrep problemet fra forskjellige vinkler. Mens Newton nærmet seg problemet via momentanhastighetsproblemet, prøvde Leibniz å løse det geometrisk ved hjelp av tangentproblemet. Arbeidene deres tillot en abstraksjon fra den rent geometriske beskrivelsen, og regnes derfor som begynnelsen av matematisk analyse. De ble først og fremst kjent gjennom boka til adelsmannen Guillaume François Antoine, marquis de L'Hôpital, som fikk privatundervisning av Johann Bernoulli og publiserte dennes forskning innen analyse. De derivasjonsreglene som er best kjent i dag, er først og fremst basert på verkene til Leonhard Euler, som satte sitt preg på funksjonsbegrepet. Newton og Leibniz arbeidet med vilkårlig små tall, men som er større enn null. Dette ble kritisert av samtidige som ulogisk, eksempelvis av biskop Berkeley i det polemiske skriftet The analyst: or a discourse addressed to an infidel mathematician. Differensialregningen ble likevel, tross den herskende usikkerheten, konsekvent videreutviklet, i første rekke på grunn av de tallrike anvendelsene i fysikk og andre områder av matematikken. Symptomatisk for den tiden var prisutskrivningen til Det prøyssiske vitenskapsakademiet i 1784:

… Den høyere geometri benytter ofte uendelig store og uendelig små størrelser; imidlertid har de gamle lærde omhyggelig unngått det uendelige, og enkelte berømte analytikere i vår tid bekjenner at begrepene er selvmotsigende. Akademiet forlanger altså at man forklarer hvordan så mange sanne satser kan oppstå av en selvmotsigende antagelse, og at man angir et sikkert og klart grunnbegrep som kan erstatte det uendelige, uten å gjøre utregningene for vanskelige eller lange …

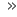
Først på begynnelsen av 1800-tallet lyktes det Augustin Louis Cauchy å gi differensialregningen den logiske stringensen vi er vant til i dag, i det han gikk bort fra de infinitesimale størrelsene og definerte den deriverte som grenseverdien til stigningen av sekantene. Den definisjonen av grenseverdier som brukes i dag ble formulert av Karl Weierstraß på slutten av 1800-tallet.

Se også

• Retningsderivert
• Lie-derivert
• Kovariant derivasjon

Referanser

Litteratur

T.M. Apostol (1969). Calculus. II. New York: John Wiley & Sons. ISBN 0-471-00008-6. 

• E.J.Borowski, J.M.Borwein (1989). Dictionary of mathematics. Glasgow: Collins. ISBN 0-00-434347-6. 
• T. Lindstrøm (2006). Kalkulus (norsk). Universitetsforlaget. ISBN 978-82-15-00977-3. Besøkt 30. august 2016. 
• S.B. Lindström (2013). Matematisk ordbok för högskolan: engelsk-svensk, svensk-engelsk: (svensk). Stefan B. Lindström. ISBN 978-91-981287-0-3. Besøkt 30. august 2016. 
• G. Thomas, R. Finney (1995). Calculus and Analytic Geometry (5th edition utg.). Reading, USA: Addison-Wesley. ISBN 0-201-53174-7. CS1-vedlikehold: Ekstra tekst (link)
• R.V Churchill, J.W. Brown, R.F. Verhey (1974). Complex variables and applications (english). Tokyo: McGraw-Hill Kogakusha. ISBN 0-07-010855-2. CS1-vedlikehold: Flere navn: forfatterliste (link)
• Florian Cajori (2007). A history of mathematical notations. I og II. Princeton, USA: Cosimo. ISBN 978-1-60206-684-7. 

Eksterne lenker

• Function calculator
• Kalkulator som kan derivere funksjoner av én variabel