De Moivres formel

De Moivres formel er et matematisk uttrykk som forbinder komplekse tall med trigonometri. Den sier at for hvert reelt tall x og heltall n har man sammenhengen

${\displaystyle (\cos x+i\sin x)^{n}=\cos nx+i\sin nx}$

hvor i er den imaginær enhet, det vil si i² = -1.

En indirekte utgave av formelen ble først publisert av Abraham de Moivre på begynnelsen av 1700-tallet, men ble mer systematisk formulert av Leonhard Euler noen tiår senere. Den er da en direkte konsekvens av Eulers formel ${\displaystyle e^{ix}=\cos x+i\sin x}$ og egenskapen ${\displaystyle (e^{ix})^{n}=e^{inx}}$ til eksponentialfunksjonen.

Formelen kan utvides til å gjelde for det mer generelle tilfellet der n er et rasjonalt tall. Den man da benyttes til å beregne n-te enhetsrøtter, det vil si komplekse løsninger av ligningen zⁿ = 1. Historisk har disse spilt en viktig rolle innen tallteori.

Noen anvendelser

Når n = 2 sier formelen at

${\displaystyle (\cos x+i\sin x)^{2}=\cos ^{2}x+2i\sin x\cos x-\sin ^{2}x=\cos 2x+i\sin 2x}$

Ved å sammenligne de reelle og imaginære leddene på begge sider, finner man sammenhengene

${\displaystyle {\begin{aligned}\cos 2x&=\cos ^{2}x-\sin ^{2}x\\\sin 2x&=2\sin x\cos x\end{aligned}}}$

De er to av de viktigste, trigonometriske identitetene.

På samme måte kan binomialformelen benyttes for n = 3 og gir

${\displaystyle (\cos x+i\sin x)^{3}=\cos ^{3}x+3i\sin x\cos ^{2}x-3\sin ^{2}x\cos x-i\sin ^{3}x=\cos 3x+i\sin 3x}$

Nå betyr dette at

${\displaystyle {\begin{aligned}\cos 3x&=4\cos ^{3}x-3\cos x\\\sin 3x&=3\sin x-4\sin ^{3}x\end{aligned}}}$

som man finner etter å ha benyttet Pythagoras' setning ${\displaystyle \sin ^{2}x+\cos ^{2}x=1.}$ Slik kan man fortsette og finne uttrykk for ${\displaystyle \sin nx}$ og ${\displaystyle \cos nx}$ ved enklere, trigonometriske funksjoner.^[1]

Enhetsrøtter

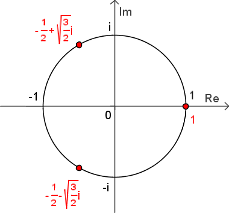
Da cosnφ = 1 og sinnφ = 0 når φ = 2π k/n når både k og n er heltall, gir de Moivres formel at løsningene til ligningen zⁿ = 1 med z = cosφ + i sinφ er gitt som

${\displaystyle z=\cos {2\pi k \over n}+i\sin {2\pi k \over n}}$

Det finnes k slike forskjellige røtter som er verdiene til disse komplekse tallene for k = 0,1,2,..,n - 1. I det komplekse planet tilsvarer de en oppdeling av enhetssirkelen i n like store deler. Ligningen omtales derfor også som sirkeldelingsligningen.^[2]

Enhetsrøttene spiller en avgjørende rolle ved løsning av mer generelle polynomligning. For eksempel gjorde Niels Henrik Abel bruk av dem i forbindelse med løsninger av femtegradsligningen. Galois-teori sier at de alle kan reduseres til de tre basale regneartene, det vil si addisjon, multiplikasjon og rotuttrekning.^[2]

Referanser

Litteratur

• A. de Moivre, De sectione anguli, Phil. Trans. 32(374), 228–230 (1723).
• L. Euler, Introductio in analysin infinitorum, Vol I, Kap.8, §133 (1748).