CIP法

CIP法（CIPほう、英: Constrained Interpolation Profile Scheme）とは、矢部孝らによって提案された、双曲型偏微分方程式を解く高次精度差分法の一つである。CIP法は高精度差分スキームであるので、機械工学、流体、電磁気、弾性体力学などの分野で広く数値解析に使用されている。

概要

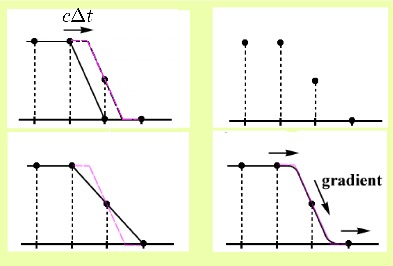数値拡散が起こる様子

CIP法では3次関数を補間関数として使用することで、双曲型問題に対して分散エラーが少ない、数値拡散が小さい、局所的な高精度補間ができる、等間隔格子を使う必要がないなどの利点が得られる。

右図で、左上の絵は移流の様子を表している。 これを格子点上の値として計算機に記憶させると右上の絵のようになる。 ここで、線形補間を行うと左下の絵のようになり、本当の波形であるピンク色の破線とはかなり開きが出てくる。 これが数値拡散であり、次の段階ではこの数値拡散によるなまりがさらに数値拡散を進展させることになる。 対して、右下の絵は傾きを考慮して補間を行っており、数値拡散が少ないことが分かる。

「CIP」とはもともとCubic Interpolated Pseudo-Particle Schemeの略であったが、研究がすすむにつれて3次多項式以外の補間関数を用いる手法へと発展した。 これにより、開発者の矢部孝は「CIP法」という名称の意味を考え直し、CIP法の本質が3次多項式を用いることにあるのではなく、元の方程式から導かれるいろいろな拘束条件をプロファイル(波の形状)に反映させることこそが本質であるとして現在の名称に変更した。よってCubic Interpolated Pseudo-Particle SchemeとConstrained Interpolation Profile Schemeのどちらも正式名称ということになる [1] [2]。

1次元移流方程式でのCIP解法

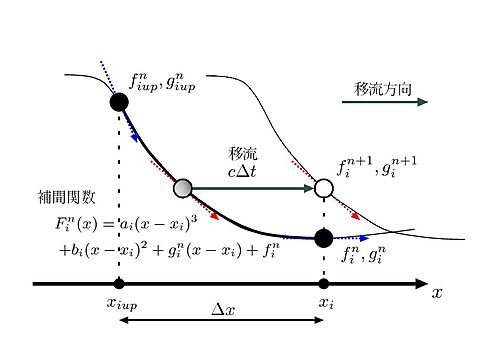CIP法計算スキームのイメージ

CIP法は1次元移流方程式を高精度に解く解法である。1次元移流方程式は次式で与えられる。

∂ f ∂ t + c ∂ f ∂ x = 0 {\displaystyle {\frac {\partial f}{\partial t}}+c{\frac {\partial f}{\partial x}}=0}

ここで、cは移流速度である。

CIP法では、格子点の値 g ( = ∂ f ∂ x ) {\displaystyle g(={\frac {\partial f}{\partial x}})} についても同時に移流計算を行うことが特徴である。 空間微分値 g {\displaystyle g} に対する移流方程式は、上の移流方程式を空間に関して微分することで得られ、以下のようになる。

∂ g ∂ t + c ∂ g ∂ x = 0 {\displaystyle {\frac {\partial g}{\partial t}}+c{\frac {\partial g}{\partial x}}=0}

時刻 n {\displaystyle n} における値 f {\displaystyle f} とその微分値 g {\displaystyle g} が格子点上の点 i {\displaystyle i} 、 i u p {\displaystyle iup} (点 i u p {\displaystyle iup} は点 i {\displaystyle i} の上流点、つまり移流速度 c > 0 {\displaystyle c>0} なら i u p = i − 1 {\displaystyle iup=i-1} である)において既知とすると、この2点間のプロファイル(つまり形状)は以下のように3次多項式で表される。 ここで、上付き添字は時刻を、下付き添字は格子点番号をあらわす。

F i n ( x ) = a i ( x − x i ) 3 + b i ( x − x i ) 2 + g i n ( x − x i ) + f i n {\displaystyle F_{i}^{n}(x)=a_{i}(x-x_{i})^{3}+b_{i}(x-x_{i})^{2}+g_{i}^{n}(x-x_{i})+f_{i}^{n}}


このようにプロファイルの補間関数を3次関数で表現することがCubicInterpolated Pseudo-Particle Schemeたる所以である。 ここで、係数 a i {\displaystyle a_{i}} 、 b i {\displaystyle b_{i}} は、

a i = g i n + g i u p n D 2 + 2 ( f i n − f i u p n ) D 3 {\displaystyle a_{i}={\frac {g_{i}^{n}+g_{iup}^{n}}{D^{2}}}+{\frac {2(f_{i}^{n}-f_{iup}^{n})}{D^{3}}}}
b i = 3 ( f i u p n − f i n ) D 2 − 2 g i n + g i u p n D {\displaystyle b_{i}={\frac {3(f_{iup}^{n}-f_{i}^{n})}{D^{2}}}-{\frac {2g_{i}^{n}+g_{iup}^{n}}{D}}}

のようになる。 ただし、移流速度 c > 0 {\displaystyle c>0} のとき D = − Δ x {\displaystyle D=-\Delta x} 、 i u p = i − 1 {\displaystyle iup=i-1} であり、移流速度 c < 0 {\displaystyle c<0} のとき D = Δ x {\displaystyle D=\Delta x} 、 i u p = i + 1 {\displaystyle iup=i+1} である。


適合条件式により、 F i n ( 0 ) = f i n {\displaystyle F_{i}^{n}(0)=f_{i}^{n}} 、 ∂ F i n ( 0 ) ∂ x = g i n {\displaystyle {\frac {\partial F_{i}^{n}(0)}{\partial x}}=g_{i}^{n}} 、 F i n ( D ) = f i u p n {\displaystyle F_{i}^{n}(D)=f_{iup}^{n}} 、 ∂ F i n ( D ) ∂ x = g i u p n {\displaystyle {\frac {\partial F_{i}^{n}(D)}{\partial x}}=g_{iup}^{n}} が成り立つので、上式において係数 a i {\displaystyle a_{i}} 、 b i {\displaystyle b_{i}} が求まる。

このように、格子点上の点において微分値 g {\displaystyle g} も与えられるので、格子間のプロファイルを3次多項式で補間することができ、精度の高い計算が可能となる。

対象とする問題は移流方程式であるので、次の時刻 n + 1 {\displaystyle n+1} での値 f i n + 1 {\displaystyle f_{i}^{n+1}} と微分値 g i n + 1 {\displaystyle g_{i}^{n+1}} は、この2点間のプロファイルを c Δ t {\displaystyle c\Delta t} だけ移動することで得られる。 つまり、 ξ = − c Δ t {\displaystyle \xi =-c\Delta t} として次式のようになる。

f i n + 1 = F i n ( ξ ) = a i ξ 3 + b i ξ 2 + g i n ξ + f i n {\displaystyle f_{i}^{n+1}=F_{i}^{n}(\xi )=a_{i}\xi ^{3}+b_{i}\xi ^{2}+g_{i}^{n}\xi +f_{i}^{n}}
g i n + 1 = ∂ F i n ( ξ ) ∂ x = 3 a i ξ 2 + 2 b i ξ + g i n {\displaystyle g_{i}^{n+1}={\frac {\partial F_{i}^{n}(\xi )}{\partial x}}=3a_{i}\xi ^{2}+2b_{i}\xi +g_{i}^{n}}

多次元問題でのCIP解法

CIP法は多次元問題での移流方程式についても適用可能である。例として、2次元での移流方程式を考えてみるが、一般に n {\displaystyle n} 次元での移流方程式にも適用できることを断っておく。


さて、2次元移流方程式は以下のように表せる。

∂ f ∂ t + C 1 ∂ f ∂ x 1 + C 2 ∂ f ∂ x 2 = 0 {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial t}}+{\boldsymbol {C}}_{1}{\frac {\partial {\boldsymbol {f}}}{\partial x_{1}}}+{\boldsymbol {C}}_{2}{\frac {\partial {\boldsymbol {f}}}{\partial x_{2}}}={\boldsymbol {0}}}

ここで、 f {\displaystyle {\boldsymbol {f}}} は変数ベクトル、 C α ( α = 1 , 2 ) {\displaystyle {\boldsymbol {C}}_{\alpha }(\alpha =1,2)} は係数マトリクスである。

2次元移流方程式にCIP法を適用する方法として、2元3次の多項式を補間関数として使う方法(A型CIP法)や方向分離解法により1次元移流方程式に落とし込んで計算する方法(M型CIP法)などが考えられる。

A型CIP法

A型CIP法では、2次元移流方程式を解くにあたり、2元3次の多項式を補間関数として用いる。 つまり、 x 1 {\displaystyle x_{1}} 軸、 x 2 {\displaystyle x_{2}} 軸からなる平面空間において、補間関数は以下のようになる。

F i , j n ( x 1 , x 2 ) = C 3 , 0 ( x 1 − x 1 i u p ) 3 + C 2 , 0 ( x 1 − x 1 i u p ) 2 + g x i , j n ( x 1 − x 1 i u p ) + f i , j n {\displaystyle F_{i,j}^{n}(x_{1},x_{2})=C_{3,0}(x_{1}-x_{1iup})^{3}+C_{2,0}(x_{1}-x_{1iup})^{2}+g_{xi,j}^{n}(x_{1}-x_{1iup})+f_{i,j}^{n}}
+ C 0 , 3 ( x 2 − x 2 j u p ) 3 + C 0 , 2 ( x 2 − x 2 j u p ) 2 + g y i , j n ( x 2 − x 2 j u p ) + C 2 , 1 ( x 1 − x 1 i u p ) 2 ( x 2 − x 2 j u p ) + C 1 , 1 ( x 1 − x 1 i u p ) ( x 2 − x 2 j u p ) + C 1 , 2 ( x 1 − x 1 i u p ) ( x 2 − x 2 j u p ) 2 {\displaystyle +C_{0,3}(x_{2}-x_{2jup})^{3}+C_{0,2}(x_{2}-x_{2jup})^{2}+g_{yi,j}^{n}(x_{2}-x_{2jup})+C_{2,1}(x_{1}-x_{1iup})^{2}(x_{2}-x_{2jup})+C_{1,1}(x_{1}-x_{1iup})(x_{2}-x_{2jup})+C_{1,2}(x_{1}-x_{1iup})(x_{2}-x_{2jup})^{2}}

ここでも、点 i u p {\displaystyle iup} と点 j u p {\displaystyle jup} はそれぞれ、点 i {\displaystyle i} と点 j {\displaystyle j} の上流点である。 また、 C {\displaystyle C} は係数であり、1次元での場合と同様に適合条件式より 格子点 ( i , j ) {\displaystyle (i,j)} 、 ( i u p , j ) {\displaystyle (iup,j)} 、 ( i , j u p ) {\displaystyle (i,jup)} の値 f n {\displaystyle f^{n}} と微分値 g n {\displaystyle g^{n}} 、格子点 ( i u p , j u p ) {\displaystyle (iup,jup)} での値 f i u p , j u p n {\displaystyle f_{iup,jup}^{n}} を用いて求められる。


A型CIP法では、点 ( i u p , j u p ) {\displaystyle (iup,jup)} において値 f n {\displaystyle f^{n}} の連続性しか要求していない。 しかし、他の3点 ( i , j ) {\displaystyle (i,j)} 、 ( i u p , j ) {\displaystyle (iup,j)} 、 ( i , j u p ) {\displaystyle (i,jup)} では 値 f n {\displaystyle f^{n}} と微分値 g n {\displaystyle g^{n}} の連続性も保証している。 このため、求めようとしている点 ( i , j ) {\displaystyle (i,j)} に対して対角線上にあり最も遠い点 ( i u p , j u p ) {\displaystyle (iup,jup)} のプロファイルが 不正確であるために、このプロファイルを持ってくるような大きな時間ステップをとってはならない。

方向分離解法

方向分離解法は一般に多次元問題を1次元問題に帰着させるために行われる。

M型CIP法

A型CIP法では補間関数の係数の数が多く、これを解析に適用しようとすると格子点上で覚えさせる値の数が多くなり、計算を行う上で合理的でない。

M型CIP法では、多次元の移流方程式に方向分離を行うことで幾つかの1次元移流方程式に帰着させ、1次元のCIPスキームで計算を行う。 方向分離解法を適用することで、上の2次元移流方程式をつぎのように分解できる。

∂ f ∂ t + C 1 ∂ f ∂ x 1 = 0 {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial t}}+{\boldsymbol {C}}_{1}{\frac {\partial {\boldsymbol {f}}}{\partial x_{1}}}={\boldsymbol {0}}}
∂ f ∂ t + C 2 ∂ f ∂ x 2 = 0 {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial t}}+{\boldsymbol {C}}_{2}{\frac {\partial {\boldsymbol {f}}}{\partial x_{2}}}={\boldsymbol {0}}}

このように方向分離を行うと、 x 1 {\displaystyle x_{1}} 方向へ分離した式を解くことによって時刻 n {\displaystyle n} の値 f n {\displaystyle {\boldsymbol {f}}^{n}} から中間の値 f ∗ {\displaystyle {\boldsymbol {f}}^{*}} が得られ、 x 2 {\displaystyle x_{2}} 方向へ分離した式を解くことによって中間の値 f ∗ {\displaystyle {\boldsymbol {f}}^{*}} から時刻 n + 1 {\displaystyle n+1} の値 f n + 1 {\displaystyle {\boldsymbol {f}}^{n+1}} が得られる。


M型CIP法で x α {\displaystyle x_{\alpha }} 方向への移流計算を行うとき、ベクトル f {\displaystyle {\boldsymbol {f}}} と x α {\displaystyle x_{\alpha }} 方向の空間微分値 ∂ f ∂ x α {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial x_{\alpha }}}} については1節の1次元CIPスキームを使って解くことが出来るが、 x β ( α ≠ β ) {\displaystyle x_{\beta }(\alpha \neq \beta )} 方向の空間微分値 ∂ f ∂ x β {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial x_{\beta }}}} については更なる空間微分値 ∂ 2 f ∂ x α ∂ x β {\displaystyle {\frac {\partial ^{2}{\boldsymbol {f}}}{\partial x_{\alpha }\partial x_{\beta }}}} を計算していないのでCIP法を使って求めることは出来ない。 よって x β {\displaystyle x_{\beta }} 方向の空間微分値 ∂ f ∂ x β {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial x_{\beta }}}} を求めるためには線形補間を行うことで、移流計算を行う。

M   型     C I P   法   の   計   算   順   序     ( n → n + 1 ) σ i j n ∂ σ i j n ∂ x α ∂ σ i j n ∂ x β → C I P   法 → F D M σ i j ∗ ∂ σ i j ∗ ∂ x α ∂ σ i j ∗ ∂ x β σ i j ∗ ∂ σ i j ∗ ∂ x β ∂ σ i j ∗ ∂ x α → C I P   法 → F D M σ i j n + 1 ∂ σ i j n + 1 ∂ x β ∂ σ i j n + 1 ∂ x α x α   方   向   へ   の   移   流   計   算   x β   方   向   へ   の   移   流   計   算   {\displaystyle {\begin{aligned}&\qquad {\mathsf {M}}\ {\text{型}}\ \ {\mathsf {CIP}}\ {\text{法}}\ {\text{の}}\ {\text{計}}\ {\text{算}}\ {\text{順}}\ {\text{序}}\ \ \left(n\rightarrow n+1\right)\\\\&{\begin{array}{cc}{\begin{array}{c}\sigma _{ij}^{n}\\\\{\frac {\partial \sigma _{ij}^{n}}{\partial x_{\alpha }}}\\\\{\frac {\partial \sigma _{ij}^{n}}{\partial x_{\beta }}}\end{array}}{\begin{array}{c}\xrightarrow {{\mathsf {CIP}}\ {\text{法}}} \\\\\\\\\xrightarrow {\mathsf {FDM}} \\\end{array}}{\begin{array}{c}\sigma _{ij}^{*}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\alpha }}}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\beta }}}\end{array}}&{\begin{array}{c}\sigma _{ij}^{*}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\beta }}}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\alpha }}}\end{array}}{\begin{array}{c}\xrightarrow {{\mathsf {CIP}}\ {\text{法}}} \\\\\\\\\xrightarrow {\mathsf {FDM}} \\\end{array}}{\begin{array}{c}\sigma _{ij}^{n+1}\\\\{\frac {\partial \sigma _{ij}^{n+1}}{\partial x_{\beta }}}\\\\{\frac {\partial \sigma _{ij}^{n+1}}{\partial x_{\alpha }}}\end{array}}\\{\begin{array}{|c|}\hline x_{\alpha }\ {\text{方}}\ {\text{向}}\ {\text{へ}}\ {\text{の}}\ {\text{移}}\ {\text{流}}\ {\text{計}}\ {\text{算}}\ \\\hline \end{array}}&{\begin{array}{|c|}\hline x_{\beta }\ {\text{方}}\ {\text{向}}\ {\text{へ}}\ {\text{の}}\ {\text{移}}\ {\text{流}}\ {\text{計}}\ {\text{算}}\ \\\hline \end{array}}\end{array}}\end{aligned}}}

C型CIP法

M型CIP法では2階の空間微分値 ∂ 2 f ∂ x α ∂ x β ( α ≠ β ) {\displaystyle {\frac {\partial ^{2}{\boldsymbol {f}}}{\partial x_{\alpha }\partial x_{\beta }}}(\alpha \neq \beta )} を計算していなかったので、空間微分値 ∂ f ∂ x β {\displaystyle {\frac {\partial {\boldsymbol {f}}}{\partial x_{\beta }}}} を計算する際は線形補間を行っていた。 この方法ではある程度の精度は保証されるが、格子間隔を広くとった場合などには x β {\displaystyle x_{\beta }} 方向の線形補間の影響が大きく出て、CIP法によるうまみを生かしきれなくなってしまう。


そこで、格子点上の2階空間微分値 ∂ 2 f ∂ x α ∂ x β {\displaystyle {\frac {\partial ^{2}{\boldsymbol {f}}}{\partial x_{\alpha }\partial x_{\beta }}}} を覚え、 x β {\displaystyle x_{\beta }} 方向にもCIP計算を行おうというのがC型CIP法である。

C   型     C I P   法   の   計   算   順   序     ( n → n + 1 ) σ i j n ∂ σ i j n ∂ x α ∂ σ i j n ∂ x β ∂ 2 σ i j n ∂ x α ∂ x β → C I P   法 → C I P   法 σ i j ∗ ∂ σ i j ∗ ∂ x α ∂ σ i j ∗ ∂ x β ∂ 2 σ i j ∗ ∂ x α ∂ x β σ i j ∗ ∂ σ i j ∗ ∂ x β ∂ σ i j ∗ ∂ x α ∂ 2 σ i j ∗ ∂ x α ∂ x β → C I P   法 → C I P   法 σ i j n + 1 ∂ σ i j n + 1 ∂ x β ∂ σ i j n + 1 ∂ x α ∂ 2 σ i j n + 1 ∂ x α ∂ x β x α   方   向   へ   の   移   流   計   算   x β   方   向   へ   の   移   流   計   算   {\displaystyle {\begin{aligned}&\qquad {\mathsf {C}}\ {\text{型}}\ \ {\mathsf {CIP}}\ {\text{法}}\ {\text{の}}\ {\text{計}}\ {\text{算}}\ {\text{順}}\ {\text{序}}\ \ \left(n\rightarrow n+1\right)\\\\&{\begin{array}{cc}{\begin{array}{c}\sigma _{ij}^{n}\\\\{\frac {\partial \sigma _{ij}^{n}}{\partial x_{\alpha }}}\\\\{\frac {\partial \sigma _{ij}^{n}}{\partial x_{\beta }}}\\{\frac {\partial ^{2}\sigma _{ij}^{n}}{\partial x_{\alpha }\partial x_{\beta }}}\end{array}}{\begin{array}{c}\xrightarrow {{\mathsf {CIP}}\ {\text{法}}} \\\\\\\\\\\xrightarrow {{\mathsf {CIP}}\ {\text{法}}} \\\\\end{array}}{\begin{array}{c}\sigma _{ij}^{*}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\alpha }}}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\beta }}}\\{\frac {\partial ^{2}\sigma _{ij}^{*}}{\partial x_{\alpha }\partial x_{\beta }}}\end{array}}&{\begin{array}{c}\sigma _{ij}^{*}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\beta }}}\\\\{\frac {\partial \sigma _{ij}^{*}}{\partial x_{\alpha }}}\\{\frac {\partial ^{2}\sigma _{ij}^{*}}{\partial x_{\alpha }\partial x_{\beta }}}\end{array}}{\begin{array}{c}\xrightarrow {{\mathsf {CIP}}\ {\text{法}}} \\\\\\\\\\\xrightarrow {{\mathsf {CIP}}\ {\text{法}}} \\\\\end{array}}{\begin{array}{c}\sigma _{ij}^{n+1}\\\\{\frac {\partial \sigma _{ij}^{n+1}}{\partial x_{\beta }}}\\\\{\frac {\partial \sigma _{ij}^{n+1}}{\partial x_{\alpha }}}\\{\frac {\partial ^{2}\sigma _{ij}^{n+1}}{\partial x_{\alpha }\partial x_{\beta }}}\end{array}}\\{\begin{array}{|c|}\hline x_{\alpha }\ {\text{方}}\ {\text{向}}\ {\text{へ}}\ {\text{の}}\ {\text{移}}\ {\text{流}}\ {\text{計}}\ {\text{算}}\ \\\hline \end{array}}&{\begin{array}{|c|}\hline x_{\beta }\ {\text{方}}\ {\text{向}}\ {\text{へ}}\ {\text{の}}\ {\text{移}}\ {\text{流}}\ {\text{計}}\ {\text{算}}\ \\\hline \end{array}}\end{array}}\end{aligned}}}

脚注

  1. ^ CFD最前線 p.209参照
  2. ^ http://www20.atwiki.jp/mynote/?page=CIP%20Memo

参考文献

  • 矢部孝、内海隆行、尾形陽一『CIP法 原子から宇宙までを解くマルチスケール解法』森北出版、2003年。ISBN 978-4-627-91831-3。 
  • 蔦原道久、渡利實、棚橋隆彦、矢部孝『CFD最前線』共立出版、2007年。ISBN 978-4-320-08166-6。 
  • 矢部孝, 尾形陽一, 滝沢研二:「CIP法とJavaによるCGシミュレーション」、森北出版、ISBN 978-4627919112、(2007年2月17日）。
  • 肖鋒, 小野寺直幸, 伊井仁志: 「計算流体力学―CIPマルチモーメント法による手法」、コロナ社、ISBN 978-4339045970（2009年3月）。
  • 日本応用数理学会「応用数理」、Vol.18, No.2 (2008), (CIP法特集号）。
  • 日本建築学会 (編)：「はじめての音響数値シミュレーションプログラミングガイド」（第6章：CIP(constrained interpolation profile)法）、コロナ社、ISBN 978-4339008388（2012年11月）。

関連項目