ザイフェルト–ファン・カンペンの定理

数学において、ザイフェルト-ファン・カンペンの定理（英: Seifert–van Kampen theorem）とは、代数トポロジーにおける定理であって、位相空間 ${\displaystyle X}$ の基本群の構造を、${\displaystyle X}$ を被覆する弧状連結な開部分空間の基本群によって表現するものである。この名前はヘルベルト・ザイフェルトとエグバート・ファン・カンペンに因む。しばしば単にファン・カンペンの定理とも呼ばれる。これはしたがってより単純な空間から組み立てられた空間の基本群を計算する為に使用することができる。

基本群に関するファン・カンペンの定理^[1]

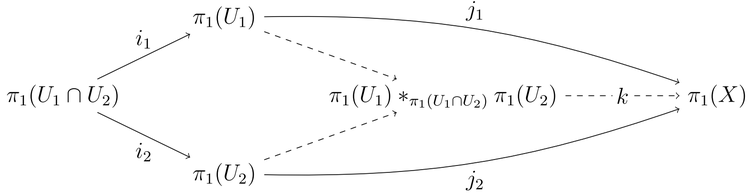
${\displaystyle X}$ を位相空間であって、2つの弧状連結な開部分空間 ${\displaystyle U_{1}}$ と ${\displaystyle U_{2}}$ の和集合になっているものとする。${\displaystyle U_{1}\cap U_{2}}$ は弧状連結かつ非空と仮定し、${\displaystyle x_{0}}$ は ${\displaystyle U_{1}\cap U_{2}}$ の点で、基本群の基点に用いられるものとする。${\displaystyle U_{1}}$ と ${\displaystyle U_{2}}$ から ${\displaystyle X}$ への包含写像は群準同型 ${\displaystyle j_{1}\colon \pi _{1}(U_{1},x_{0})\to \pi _{1}(X,x_{0})}$ と ${\displaystyle j_{2}\colon \pi _{1}(U_{2},x_{0})\to \pi _{1}(X,x_{0})}$ を誘導する。すると ${\displaystyle X}$ は弧状連結であり、${\displaystyle j_{1}}$ と ${\displaystyle j_{2}}$ は可換なプッシュアウト（英語版）図式を成す：

自然な射 ${\displaystyle k}$ は同型である。つまり ${\displaystyle X}$ の基本群は ${\displaystyle U_{1}}$ と ${\displaystyle U_{2}}$ の基本群の自由積を ${\displaystyle \pi _{1}(U_{1}\cap U_{2},x_{0})}$ で融合したものにほかならない^[2]。

通常、包含によって誘導される射は単射ではなく、この言明のより精密なバージョンは群のプッシュアウト（英語版）の言葉を用いて書かれる。

基本亜群に関するファン・カンペンの定理

円は代数トポロジーに於ける最も重要かつ基本的な例であるが、残念ながら上で与えた定理は円の基本群を計算できない。その理由は、円は連結な共通部分を持つような2つの開集合の和集合としては実現し得ないということにある。この問題は、幾何学的な状況に応じて選択をした基点の成す集合 ${\displaystyle A}$ 上の基本亜群 ${\displaystyle \pi _{1}(X,A)}$ を用いることによって解決することができる。円の場合には、2つの基点を選べばよい^[3]。

この亜群は ${\displaystyle A\cap X}$ の点を結ぶ ${\displaystyle X}$ 内の曲線達の両端に相対的（両端を固定する）ホモトピー類からなる。とくに、${\displaystyle X}$ が可縮空間で、${\displaystyle A}$ が ${\displaystyle X}$ の相異なる2点からなるとき、${\displaystyle \pi _{1}(X,A)}$ は ${\displaystyle {\mathcal {I}}}$ としばしば書かれる亜群に同型であることが容易に見て取れる。この亜群は2つの頂点と各頂点間にちょうどひとつの射からなる。この亜群は、群の理論に於ける整数の成す群が果たすのと同様の役割を、亜群の理論に於いて果たす^[4]。亜群 ${\displaystyle {\mathcal {I}}}$ はまた亜群のホモトピーの概念を考えることを可能にする：つまりこれは亜群の圏に於ける単位区間対象である。

亜群の圏は全ての余極限、とくに全てのプッシュアウトを持つ。

定理. 位相空間 ${\displaystyle X}$ が2つの部分空間 ${\displaystyle X_{1}}$ と ${\displaystyle X_{2}}$ の内部によって被覆され、基点集合 ${\displaystyle A}$ は ${\displaystyle X_{1}}$ と ${\displaystyle X_{2}}$ と ${\displaystyle X_{0}=X_{1}\cap X_{2}}$ の全ての弧状連結成分と交わりを持つとする。このとき ${\displaystyle A}$ は ${\displaystyle X}$ の全ての弧状連結成分と交わり、かつ包含によって誘導された射からなる図式 ${\displaystyle P}$

は亜群の圏のプッシュアウト図式となる^[5]。

この定理は、基本亜群 ${\displaystyle \pi _{1}(X,A)}$ の完全な決定に際し、トポロジーから代数への移行手段を与える。代数および組合せ論を、幾つかの基点における基本群の決定に用いる必要がある。

この定理のひとつの解釈は、これがホモトピー1-型を計算するというものである。

同値な定式化

組み合わせ群論の言葉を用いるなら、${\displaystyle X}$ が位相空間、${\displaystyle U}$ と ${\displaystyle V}$ が ${\displaystyle X}$ の弧状連結な開部分空間、${\displaystyle U\cap V}$ が空でなく弧状連結、そして${\displaystyle w\in U\cap V}$ ならば、${\displaystyle \pi _{1}(X,w)}$ は ${\displaystyle \pi _{1}(U,w)}$ と ${\displaystyle \pi _{1}(V,w)}$ の（必ずしも単射ではない）準同型 ${\displaystyle I\colon \pi _{1}(U\cap V,w)\to \pi _{1}(U,w)}$ と ${\displaystyle J\colon \pi _{1}(U\cap V,w)\to \pi _{1}(V,w)}$ による融合積である、と言うことができる。群の表示

${\displaystyle {\begin{aligned}\pi _{1}(U,w)&=\langle u_{1},\cdots ,u_{k}\mid \alpha _{1},\cdots ,\alpha _{l}\rangle \\\pi _{1}(V,w)&=\langle v_{1},\cdots ,v_{m}\mid \beta _{1},\cdots ,\beta _{n}\rangle \\\pi _{1}(U\cap V,w)&=\langle w_{1},\cdots ,w_{p}\mid \gamma _{1},\cdots ,\gamma _{q}\rangle \end{aligned}}}$

が与えられたならば、その融合積は次のように表示できる^[6]。

${\displaystyle \pi _{1}(X,w)=\langle u_{1},\cdots ,u_{k},v_{1},\cdots ,v_{m}\mid \alpha _{1},\cdots ,\alpha _{l},\beta _{1},\cdots ,\beta _{n},I(w_{1})J(w_{1})^{-1},\cdots ,I(w_{p})J(w_{p})^{-1}\rangle .}$

圏論では、${\displaystyle \pi _{1}(X,w)}$ は群の圏における次の図式のプッシュアウト（英語版）である：

${\displaystyle \pi _{1}(U,w)\gets \pi _{1}(U\cap V,w)\to \pi _{1}(V,w).}$

例

2-球

ファン・カンペンの定理はより簡単な空間に分解できるような位相空間の基本群の計算に利用できる。例として球 ${\displaystyle S^{2}}$ を考えよう。開集合 ${\displaystyle A=S^{2}\setminus \{n\}}$ と ${\displaystyle B=S^{2}\setminus \{s\}}$ を選ぶ。ここで n と s はそれぞれ北極と南極を表す。すると、A, B および A ∩ B は弧状連結な開集合であることが分かる。よって、A ∩ B から A と B への包含と、A と B から ${\displaystyle S^{2}}$ への包含からなる可換図式が存在すること、および、それに対応する各々の部分空間の基本群の間の準同型からなる図式が存在することが分かる。ファン・カンペンの定理を適用することによって

${\displaystyle \pi _{1}(S^{2})=\pi _{1}(A)\cdot \pi _{1}(B)/\ker(\Phi )}$

という結果を得る。しかし、A と B はどちらも ${\displaystyle \mathbb {R} ^{2}}$（これは単連結）に同相であるから、A と B はともに自明な基本群を持つ。このことから明らかに、${\displaystyle S^{2}}$ の基本群は自明である。

空間の楔和

2つの基点付き位相空間 ${\displaystyle (X,x)}$ と ${\displaystyle (Y,y)}$ が与えられると、その楔和 ${\displaystyle (X\vee Y,p)}$ を ${\displaystyle X\amalg Y}$ の2つの基点を同一視する商を取ることで構成できる。

点（がひとつだけからなる空間）の基本群は自明であるから、ファン・カンペンの定理は

${\displaystyle \pi _{1}(X\vee Y,p)\cong \pi _{1}(X,x)*\pi _{1}(Y,y)}$

が群の同型であることを示す。

向き付けられた種数 g の曲面

より複雑な例としては種数 n の向き付け可能曲面 S の基本群（種数 n の曲面群としても知られる）の計算がある。S はその基本多角形（英語版）を使って構成できる。まず１つ目の開集合 A を決める為に、この多角形の中に収まるような円盤を取る。そして B を A の中心点の S における補集合とする。すると A と B の共通部分は円環領域となる。これは円周とホモトピー同値であり同じ基本群を持つことが知られている。よって ${\displaystyle \pi _{1}(A\cap B)=\pi _{1}(S^{1})}$ （これは整数の成す加群）であり、${\displaystyle \pi _{1}(A)=\pi _{1}(D^{2})={1}}$ である。すると ${\displaystyle \pi _{1}(A\cap B)}$ から ${\displaystyle \pi _{1}(A)}$ への包含はどの生成元も自明な元に送る。しかし、${\displaystyle \pi _{1}(A\cap B)}$ から ${\displaystyle \pi _{1}(B)}$ への包含は自明でない。このことを理解する為に、まず ${\displaystyle \pi _{1}(B)}$ を計算しなければならない。これは ${\displaystyle \pi _{1}(B)}$（S から一点を除いたもの）を基本多角形の辺へと変形レトラクトすることができるから容易である。この辺は

${\displaystyle A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}A_{2}^{-1}B_{2}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}}$

とラベル付けられているとしよう。この（変形レトラクトされた後の）空間は 2n 個の円周の楔和（円を束ねたブーケとも呼ばれる）であることが知られており、これはさらに 2n 個の生成元を持つ自由群と同型な基本群を持つことが知られている。この場合、それらの生成元は（上でラベル付けしたところの）辺たちによって表現できる：${\displaystyle \{A_{1},B_{1},\cdots ,A_{n},B_{n}\}}$。いまやファン・カンペンの定理を適用するに十分な情報を得た。生成元はループ ${\displaystyle \{A_{1},B_{1},\cdots ,A_{n},B_{n}\}}$ であり（A は単連結であるから生成元を持たないことが帰結する）、そしてちょうどひとつの関係式

${\displaystyle A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}A_{2}^{-1}B_{2}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}=1}$

がある。この生成元と関係式とを用いて、この群は

${\displaystyle \langle A_{1},B_{1},\cdots ,A_{n},B_{n}\mid A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}\rangle }$

と記述できる。

一般化

後述の通り、この定理はロナルド・ブラウンによって、基点集合 ${\displaystyle A}$ 上の基本亜群 ${\displaystyle \pi _{1}(X,A)}$ を用いることで、不連結な場合へと一般化された。任意の被覆に対する（ただし ${\displaystyle A}$ はその被覆に含まれる任意の3つの集合の共通部分と交わるという制限のもとでの）この定理はブラウンとアブドゥル・ラザク・サラーの論文で与えられている^[7]。

関連項目

• 高次代数
• 高次圏論
• 擬円（英語版）
• ロナルド・ブラウン (数学者)（英語版）

脚注

参考文献

• Allen Hatcher, Algebraic topology. (2002) Cambridge University Press, Cambridge, xii+544 pp. ISBN 0-521-79160-X, 0-521-79540-0
• Peter May, A Concise Course in Algebraic Topology. (1999) University of Chicago Press, ISBN 0-226-51183-9 (Section 2.7 provides a category-theoretic presentation of the theorem as a colimit in the category of groupoids).
• Higher-dimensional algebra
• Ronald Brown, Groupoids and Van Kampen's theorem, Proc. London Math. Soc. (3) 17 (1967) 385-401.
• Mathoverflow discussion on many base points
• Ronald Brown, Topology and groupoids (2006) Booksurge LLC ISBN 1-4196-2722-8
• R. Brown and A. Razak, A van Kampen theorem for unions of non-connected spaces, Archiv. Math. 42 (1984) 85-88. (This paper gives probably the optimal version of the theorem, namely the groupoid version of the theorem for an arbitrary open cover and a set of base points which meets every path component of every 1-.2-3-fold intersections of the sets of the cover.)
• P.J. Higgins, Categories and groupoids (1971) Van Nostrand Reinhold
• Ronald Brown, Higher-dimensional group theory (2007) (Gives a broad view of higher-dimensional van Kampen theorems involving multiple groupoids).
• Seifert, H., Konstruction drei dimensionaler geschlossener Raume. Berichte Sachs. Akad. Leipzig, Math.-Phys. Kl. (83) (1931) 26–66.
• E. R. van Kampen. On the connection between the fundamental groups of some related spaces. American Journal of Mathematics, vol. 55 (1933), pp. 261–267.
• Brown, R., Higgins, P. J, On the connection between the second relative homotopy groups of some related spaces, Proc. London Math. Soc. (3) 36 (1978) 193–212.
• Brown, R., Higgins, P. J. and Sivera, R.. 2011, EMS Tracts in Mathematics Vol.15 (2011) Nonabelian Algebraic Topology: filtered spaces, crossed complexes, cubical homotopy groupoids; (The first of three Parts discusses the applications of the 1- and 2-dimensional versions of the Seifert–van Kampen Theorem. The latter allows calculations of nonabelian second relative homotopy groups, and in fact of homotopy 2-types. The second part applies a Higher Homotopy van Kampen Theorem for crossed complexes, proved in Part III.)
• Van Kampen's theorem result - PlanetMath.org（英語）
• R. Brown, H. Kamps, T. Porter : A homotopy double groupoid of a Hausdorff space II: a van Kampen theorem', Theory and Applications of Categories, 14 (2005) 200–220.
• Dylan G.L. Allegretti, Simplicial Sets and van Kampen's Theorem (Discusses generalized versions of van Kampen's theorem applied to topological spaces and simplicial sets).
• R. Brown and J.-L. Loday, ``Van Kampen theorems for diagrams of spaces, Topology 26 (1987) 311–334.

この記事は、クリエイティブ・コモンズ・ライセンス 表示-継承 3.0 非移植のもと提供されているオンライン数学辞典『PlanetMath』の項目Van Kampen's theoremの本文を含む