Lunghezza di un arco

In matematica, la lunghezza di un arco è un numero reale positivo che misura intuitivamente l'estensione di un arco o di una curva.

Nonostante la definizione di lunghezza di un segmento o di un percorso poligonale sia stata chiara da tempo, una definizione generale soddisfacente della lunghezza d'arco è relativamente recente. Questo problema, noto anche come rettificazione, è stato inizialmente affrontato per curve specifiche e successivamente risolto grazie al calcolo infinitesimale. La definizione risultante, accettata adesso da tutti i matematici, funziona per un insieme molto vasto di curve, dette rettificabili.

Definizione

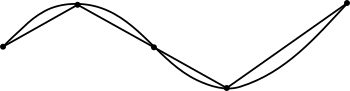
Scelto un numero finito di punti lungo la curva e connettendo ogni punto al successivo con un segmento, la somma delle lunghezze dei segmenti è la lunghezza del "cammino poligonale". La lunghezza del segmento sarà definita come la distanza tra i due estremi.

La lunghezza della curva è il più piccolo numero che la lunghezza del cammino poligonale non può superare, ovvero è l'estremo superiore della lunghezza del cammino della poligonale, al variare delle poligonali.

In termini matematici sia ${\displaystyle \varphi :[a,b]\to X}$ la curva e ${\displaystyle (X,d)}$ uno spazio metrico con la distanza d. Per definire la poligonale bisogna scegliere i punti sulla curva. Sia quindi ${\displaystyle \rho }$ una partizione dell'intervallo ${\displaystyle [a,b]}$

${\displaystyle \rho =\{t_{i}\in [a,b]:a=t_{0}<t_{1}<\ldots <t_{n}=b\}}$

La lunghezza della poligonale, è:

${\displaystyle d(\varphi (t_{0}),\varphi (t_{1}))+\cdots +d(\varphi (t_{n-1}),\varphi (t_{n}))=\sum _{i=1}^{n}d(\varphi (t_{i}),\varphi (t_{i-1}))}$

e la lunghezza della curva è l'estremo superiore di questa quantità al variare della partizione:

${\displaystyle L(\varphi )=\sup _{\rho }\sum _{i=1}^{n}d(\varphi (t_{i}),\varphi (t_{i-1}))}$

Se tale valore non è infinito, la curva si dice rettificabile. Le curve di Peano e di Koch non sono rettificabili. La lunghezza di una curva non dipende dalla sua parametrizzazione.

Calcolo

Se una curva è derivabile con continuità allora è rettificabile: per ogni punto t dell'intervallo è definita una velocità e si può dimostrare che la lunghezza definita come sopra è uguale all'integrale di questa velocità su I (quando la curva è in forma parametrica):

${\displaystyle L(\varphi )=\int _{I}||\varphi ^{\prime }{(t)}||\mathrm {d} t}$

dove ${\displaystyle ||\cdot ||}$ è la norma indotta dalla distanza usata nella definizione sopra. Usando la nozione di integrale di linea si può scrivere anche:

${\displaystyle L(\varphi )=\int _{\varphi }\mathrm {d} l.}$

Grafico di una funzione

A volte è utile conoscere la lunghezza del grafico di una funzione ${\displaystyle f:[a,b]\to \mathbb {R} }$. In questo caso il grafico si può scrivere come curva ${\displaystyle \varphi :[a,b]\to \mathbb {R} ^{2}}$:

${\displaystyle \left\{{\begin{matrix}x=t\\y=f(t)\end{matrix}}\right.\quad t\in [a,b]}$

Usando la definizione integrale di lunghezza di arco si perviene al risultato (quando la curva è in forma cartesiana):

${\displaystyle L(\varphi )=\int _{a}^{b}{\sqrt {1+[f'(t)]^{2}}}\,\mathrm {d} t.}$

Se la curva bidimensionale è parametrica con x=f(t) e y=g(t), la lunghezza dell'arco è

${\displaystyle s=\int _{a}^{b}{\sqrt {[f'(t)]^{2}+[g'(t)]^{2}}}\,\mathrm {d} t.}$

Se invece la curva è tridimensionale, con x=f(t), y=g(t), z=k(t), la lunghezza dell'arco è

${\displaystyle s=\int _{a}^{b}{\sqrt {[f'(t)]^{2}+[g'(t)]^{2}+[k'(t)]^{2}}}\,\mathrm {d} t.}$

Per dimensioni più alte si procede analogamente.

Storia

Antichità

Durante la storia della matematica, per molto tempo, anche le menti migliori considerarono impossibile calcolare la lunghezza di un arco irregolare. Nonostante Archimede fosse stato pioniere con l'approssimazione rettangolare per trovare l'area sotto una curva con il suo metodo di esaustione, pochi credevano che fosse possibile che le curve avessero una lunghezza definita come le linee diritte. Come spesso avviene nel calcolo i primi risultati furono ottenuti come approssimazioni. Molti iniziarono a inscrivere i poligoni con delle curve e a calcolare la lunghezza dei lati. Usando sempre più lati e usando lati più piccoli, furono in grado di ottenere approssimazioni via via più accurate.

XVII secolo

Nel 1600, il metodo d'esaustione consentì di rettificare con metodi geometrici molte curve trascendenti: la spirale logaritmica da parte di Evangelista Torricelli nel 1645 (alcune fonti dicono John Wallis negli anni 1650), la cicloide da parte di Christopher Wren nel 1658, e la catenaria da parte di Gottfried Leibniz nel 1691.

Forma integrale

Prima del completo sviluppo del calcolo, le basi per la moderna lunghezza degli archi sotto forma di integrale furono scoperte indipendentemente da Hendrik van Heuraet e Pierre Fermat.

Nel 1659 van Heuraet pubblicò una costruzione mostrando che la lunghezza di un arco poteva essere interpretata come l'area sotto una curva, e lo applicò alla parabola. Nel 1660, Fermat pubblicò una teoria più generale che conteneva gli stessi risultati nel suo De linearum curvarum cum lineis rectis comparatione dissertatio geometrica.

Partendo dai suoi lavori sulle tangenti, Fermat usò la curva

${\displaystyle y=x^{3/2}}$

la cui tangente in x = a ha pendenza:

${\displaystyle {3 \over 2}a^{1/2}}$

quindi la retta tangente ha equazione

${\displaystyle y={3 \over 2}{a^{1/2}}(x-a)+f(a).}$

Successivamente, incrementò a di una piccola quantità a a + ε, facendo diventare il segmento AC una buona approssimazione per la lunghezza della curva da A a D. Per trovare la lunghezza del segmento AC usò il teorema di Pitagora:

${\displaystyle {\begin{aligned}AC^{2}&{}=AB^{2}+BC^{2}\\&{}=\varepsilon ^{2}+{9 \over 4}a\varepsilon ^{2}\\&{}=\varepsilon ^{2}\left(1+{9 \over 4}a\right)\end{aligned}}}$

che porta a

${\displaystyle AC=\varepsilon {\sqrt {1+{9 \over 4}a\ }}.}$

Per approssimare la lunghezza, Fermat sommò in una sommatoria di segmenti piccoli. Notare che il risultato moderno è:

${\displaystyle \int _{\alpha }^{\beta }{\sqrt {1+{\frac {9}{4}}x}}\,\mathrm {d} x}$

Altri progetti

• Wikimedia Commons contiene immagini o altri file su lunghezza di un arco

Collegamenti esterni

• (EN) Matematica prima del calcolo (PDF), su math.kennesaw.edu. URL consultato il 10 maggio 2006 (archiviato dall'url originale il 19 dicembre 2005).
• (EN) La storia della curvatura, su brown.edu. URL consultato il 2 maggio 2019 (archiviato dall'url originale il 5 aprile 2007).
• (EN) Calculus Study Guide – Arc Length (Rectification), su pinkmonkey.com.
• (EN) Famous Curves Index Archiviato il 13 aprile 2006 in Internet Archive. The MacTutor History of Mathematics archive

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica