Equazione di terzo grado

In matematica viene detta equazione di terzo grado o cubica un'equazione che si presenta o può essere trasformata in forma polinomiale in cui il grado massimo dell'incognita è il terzo. Pertanto, la sua forma canonica è

${\displaystyle ax^{3}+bx^{2}+cx+d=0,\qquad {\text{con }}a\neq 0.}$

Il primo metodo risolutivo generale per questa classe di equazioni è dovuto a Scipione del Ferro. Tuttavia, alla formula risolutiva vengono normalmente associati i nomi di Gerolamo Cardano e Niccolò Fontana detto Tartaglia, che portarono a compimento una serie di miglioramenti del metodo dovuti a vari autori della scuola algebrica italiana.

Storia

Sin dai tempi della matematica babilonese erano noti metodi risolutivi per equazioni di terzo grado particolari, essenzialmente quelle che possono essere ricondotte ad un'equazione di secondo grado. I greci riuscivano a risolvere alcune equazioni di terzo grado con il metodo delle coniche, metodo reso famoso dall'aneddoto della duplicazione dell'altare di Apollo. Durante l'età della matematica persiana, ʿUmar Khayyām credeva che, a parte i casi riducibili, non esistesse un metodo risolutivo generale per le equazioni di terzo grado, opinione che ancora Luca Pacioli riportava nella sua opera del 1494 Summa de arithmetica, geometria, proportioni et proportionalità.

Un primo procedimento risolutivo di buona generalità venne scoperto da Scipione del Ferro; la data esatta di questa scoperta resta ignota, ma egli la comunicò in fin di vita (ca. 1526) ad un suo allievo, Antonio Maria del Fiore, detto Floridus in latino.

Niccolò Fontana, detto Tartaglia, già nel 1541 sapeva risolvere problemi implicanti equazioni di terzo grado: quando si diffuse la voce, Floridus e Tartaglia si sfidarono a vicenda, ognuno sottoponendo all'altro trenta "questioni" da risolvere entro una certa data. Quando arrivò il giorno stabilito, Tartaglia aveva risolto tutti i problemi di Floridus e questi nemmeno uno. All'epoca infatti i numeri negativi non venivano usati e si ricorreva a diversi metodi risolutivi con soli numeri positivi: Floridus conosceva solamente un metodo per coefficienti positivi, ossia per equazioni della forma:

${\displaystyle x^{3}+px=q,}$

mentre Tartaglia gli aveva sottoposto tutti problemi con coefficienti negativi, e nella forma:

${\displaystyle x^{3}+px^{2}=q,}$

probabilmente riconducendo questo caso al precedente. Era infatti noto che, se il coefficiente di terzo grado è l'unità, allora quello di secondo grado cambiato di segno è la somma delle radici.

Sorse poi nel 1545 un'aspra polemica tra Tartaglia, Gerolamo Cardano e Lodovico Ferrari, cui si deve la soluzione generale dell'equazione di quarto grado, circa la paternità della soluzione. Venuto a sapere della vittoria su Floridus, Cardano aveva invitato Tartaglia a recarsi da lui nella città di Milano, con la vaga promessa di trovargli un mecenate. Tartaglia non aveva fonti di reddito stabili forse a causa della balbuzie, causatagli da una sciabolata ricevuta da ragazzo durante l'assalto di Brescia da parte di truppe francesi nel 1512. Il difetto, a cui si deve anche il soprannome autoimpostosi di Tartaglia, lo rendeva inadatto all'insegnamento, per cui l'offerta venne accettata. Tartaglia dunque rivelò a Cardano il procedimento sotto forma di poesia (tra parentesi la notazione attuale):

Successivamente Tartaglia sosterrà di aver fatto giurare a Cardano che non l'avrebbe mai reso pubblico ma il fatto è contestato dallo stesso Cardano. Cardano e Ferrari a quel punto lavorarono sul materiale fornito loro dal Tartaglia, andando oltre le sue scoperte e riuscendo a fornire una dimostrazione rigorosa della soluzione; è proprio in questo periodo che Ferrari risolve l'equazione di quarto grado. Il procedimento risolutivo individuato dal matematico bolognese richiedeva però la soluzione dell'equazione di terzo grado scoperta da Tartaglia, e che non poteva essere pubblicata a causa della promessa fatta da Cardano. Dopo qualche tempo tuttavia, quest'ultimo venne a sapere delle precedenti deduzioni di Scipione del Ferro e si recò quindi presso Annibale della Nave, genero di del Ferro e suo successore alla cattedra di matematica dell'Università di Bologna, nella speranza di riuscire a carpire le informazioni di cui aveva bisogno. Della Nave mostrò a Cardano il manoscritto sul quale il suocero aveva annotato la soluzione dell'equazione, la stessa trovata da Tartaglia; fu così che Cardano, sentendosi svincolato dalla promessa fatta, pubblicò il risultato noto come "formula di Cardano" nell'Ars magna.^[1] Tenendo presente dalla poesia di Tartaglia che ${\displaystyle x={\sqrt[{3}]{u}}-{\sqrt[{3}]{v}}}$ esprimendo il procedimento in un'unica formula si ottengono le note "formule cardaniche":

${\displaystyle x^{3}+px+q=0\quad \Rightarrow \quad x={\sqrt[{3}]{-{q \over 2}+{\sqrt[{2}]{{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt[{2}]{{q^{2} \over 4}+{p^{3} \over 27}}}}}.}$

Talvolta risulta comodo scrivere l'equazione nella forme equivalenti rispettivamente rinascimentale e moderna:

${\displaystyle x^{3}=3{\dot {p}}x+2{\dot {q}}\qquad }$ e ${\displaystyle \qquad x^{3}-3{\dot {p}}x-2{\dot {q}}=0}$

nelle quali sono state introdotte

${\displaystyle {\dot {p}}=-{p \over 3}\qquad }$ e ${\displaystyle \qquad {\dot {q}}=-{q \over 2}}$

segnate col puntino esclusivamente per evitare equivoci con le altre formule. In questo modo la formula di Cardano assume la forma più semplice:

${\displaystyle x={\sqrt[{3}]{{\dot {q}}+{\sqrt[{2}]{{\dot {q}}^{2}-{\dot {p}}^{3}}}}}+{\sqrt[{3}]{{\dot {q}}-{\sqrt[{2}]{{\dot {q}}^{2}-{\dot {p}}^{3}}}}}.}$

Pur se figlio illegittimo, astrologo, eretico e giocatore incallito, Cardano era un rispettabile professore a Bologna e Milano, tanto che ebbe una pensione dal Papa. Egli fu uno scrittore prolifico nel campo della medicina, delle scienze naturali e della matematica. Con l'uscita dell'Artis Magnae sive de regulis algebraicis nel 1545, in cui vennero pubblicate le soluzioni per le equazioni di terzo e quarto grado, pur riconoscendo la paternità delle rispettive scoperte a Ferrari e Tartaglia, divampò la polemica con Tartaglia. Infatti questo non fu sufficiente per evitare le ire di Tartaglia che offese pubblicamente Cardano chiamandolo "huomo di poco sugo"^[2]. Ferrari difese accanitamente il maestro e ne seguì una lunga disputa (dalla quale, comunque, Cardano si mantenne sempre neutrale). Sfidato pubblicamente da Ferrari, Tartaglia fu umiliato e sconfitto e poco dopo vide il ritiro del suo incarico di professore.

Cardano e Ferrari divennero improvvisamente famosi, tuttavia nemmeno la loro fortuna durò a lungo: il figlio di Cardano fu condannato a morte per l'assassinio della moglie mentre l'altro suo figlio lo derubò per saldare i suoi debiti di gioco. Egli stesso venne poi imprigionato per aver calcolato l'oroscopo di Gesù Cristo; Ferrari invece, dopo aver perso le dita di una mano in una rissa, fu probabilmente avvelenato dalla sorella.

Negli anni successivi François Viète trovò un altro metodo di risoluzione: una volta eliminato il coefficiente di secondo grado si applica la sostituzione ${\displaystyle \displaystyle {x=y-{p \over 3y}}}$ che porta a un'equazione di secondo grado nella variabile ${\displaystyle \eta =y^{3}}$.^[3]

Nuovi metodi per la soluzione di equazioni cubiche e biquadratiche furono mostrate più tardi dall'olandese Johan Jacob Ferguson nell'opera Labyrinthus algebrae.^[4]

Metodo risolutivo

Cardano, Tartaglia e altri algebristi italiani rinascimentali pubblicarono propri metodi per la risoluzione delle equazioni di terzo grado. Tempo dopo François Viète, in seguito all'introduzione dei coefficienti letterali, pubblicò nell'Isagoge in artem analyticam un metodo molto lineare, che prevede la risoluzione di un'equazione di terzo grado completa riducendola, tramite una multipla sostituzione delle variabili, a una particolare equazione quadratica. Il procedimento è il seguente.

Un'equazione del tipo

${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

si riconduce, applicando la seguente sostituzione

${\displaystyle x=y-{\frac {b}{3a}}}$

(geometricamente questa traslazione posiziona la cubica in modo che abbia il proprio flesso sull'asse delle ordinate; generalmente le equazioni di questo tipo sono simmetriche rispetto al proprio punto di flesso), alla forma

${\displaystyle y^{3}+py+q=0,}$

dove

${\displaystyle p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}\quad }$ e ${\displaystyle \quad q={\frac {d}{a}}-{\frac {bc}{3a^{2}}}+{\frac {2b^{3}}{27a^{3}}}.}$

Si ottiene così un'equazione nella forma precedentemente descritta le cui soluzioni sono ${\displaystyle y=u+v}$ dove ${\displaystyle u}$ e ${\displaystyle v}$ sono le radici:

${\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}};\quad v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Da cui si ricava che

${\displaystyle y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

La formula per calcolare le soluzioni dell'equazione di terzo grado è quindi:

${\displaystyle x=-{\frac {b}{3a}}+{\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Bisogna ricordare che per il teorema fondamentale dell'algebra un'equazione di terzo grado deve avere tre soluzioni complesse, bisogna quindi considerare anche i risultati complessi delle radici.

Ora è necessario calcolare se la quantità che sta sotto le radici quadrate, indicata con ${\displaystyle \Delta _{\text{III}}}$, è positiva o negativa.

• Se ${\displaystyle \Delta _{\text{III}}}$ è maggiore di 0, si calcolano i due numeri reali ${\displaystyle u}$ e ${\displaystyle v}$ uguali a

  ${\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}};\quad v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}},}$

  e le soluzioni dell'equazione sono:

  ${\displaystyle y_{1}=u+v;}$

  ${\displaystyle y_{2}=u\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)+v\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right);}$

  ${\displaystyle y_{3}=u\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)+v\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right).}$

• Se ${\displaystyle \Delta _{\text{III}}}$ è minore di 0 bisognerà convertire il numero complesso

  ${\displaystyle -{\frac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}}$

  nella forma trigonometrica ${\displaystyle \rho (\cos \theta +i\sin \theta )}$ e le tre soluzioni sono i risultati delle formule:

  ${\displaystyle y_{1}=2{\sqrt {-{\frac {p}{3}}}}\cos {\frac {\theta }{3}};}$

  ${\displaystyle y_{2}=2{\sqrt {-{\frac {p}{3}}}}\cos {\frac {\theta +2\pi }{3}};}$

  ${\displaystyle y_{3}=2{\sqrt {-{\frac {p}{3}}}}\cos {\frac {\theta +4\pi }{3}}.}$

• Se ${\displaystyle \Delta _{\text{III}}}$ è uguale a 0, le soluzioni dell'equazione sono:

  ${\displaystyle y_{1}=-2{\sqrt[{3}]{\frac {q}{2}}};}$

  ${\displaystyle y_{2}=y_{3}={\sqrt[{3}]{\frac {q}{2}}}.}$

Problemi relativi alle soluzioni

Cardano incontrò però alcune difficoltà, dati i metodi dell'epoca, a trattare casi come

${\displaystyle x^{3}=15x+4.}$

Infatti applicando la formula risolutiva si trova

${\displaystyle x={\sqrt[{3}]{2+11{\sqrt {-1}}}}+{\sqrt[{3}]{2-11{\sqrt {-1}}}}}$

e la radice di un numero negativo non si sapeva trattare. Però, cercando una soluzione con i metodi geometrici di ʿUmar Khayyām, si trova che una soluzione è ${\displaystyle x=4}$ e di conseguenza altre due soluzioni sono ottenibili risolvendo l'equazione

${\displaystyle x^{2}+4x+1=0.}$

Quindi l'equazione ha tre radici reali, ovvero si ha la fattorizzazione

${\displaystyle x^{3}-15x-4=(x-4)(x+2-{\sqrt {3}})(x+2+{\sqrt {3}}),}$

mentre la formula risolutiva porta a numeri non reali.

In generale si incorre in numeri non reali con equazioni della forma ${\displaystyle y^{3}+py+q}$ per le quali

${\displaystyle \left({p \over 3}\right)^{3}<-\left({q \over 2}\right)^{2}.}$

Questa disuguaglianza caratterizza quello che veniva chiamato caso irriducibile, caso ritenuto intrattabile. Gli autori posteriori (primo fra tutti Rafael Bombelli) riprenderanno questi risultati giungendo alla introduzione dei numeri complessi, entità indispensabili per disporre di un procedimento generale per la risoluzione delle equazioni di terzo grado a coefficienti reali. I numeri complessi si sono poi rivelati fondamentali per moltissimi altri sviluppi matematici, in particolare per il teorema fondamentale dell'algebra.

Dimostrazione

Trasformazione della formula generale in una formula con soluzioni note

La tecnica utilizzata per trovare la formula risolutiva di un'equazione di terzo grado è quella di trasformarla in un'equazione con soluzioni note. Se prendiamo l'identità:

${\displaystyle y=u+v}$

ed eleviamo tutto al cubo otteniamo:

${\displaystyle y^{3}=(u+v)^{3}}$

${\displaystyle y^{3}=u^{3}+3u^{2}v+3uv^{2}+v^{3}}$

${\displaystyle y^{3}=u^{3}+v^{3}+3uv(u+v)}$

${\displaystyle y^{3}=u^{3}+v^{3}+3uvy}$

${\displaystyle y^{3}-3uvy-(u^{3}+v^{3})=0.}$

Abbiamo così costruito un'equazione di terzo grado della quale conosciamo la soluzione (${\displaystyle y=u+v}$). Possiamo notare che l'equazione ottenuta non possiede il termine di secondo grado e ${\displaystyle y^{3}}$ ha coefficiente 1. I passaggi successivi avranno l'obiettivo di trasformare una classica equazione di terzo grado in un'equazione simile a quella appena costruita.

Prendiamo quindi l'equazione di terzo grado e dividiamo tutti i termini per la costante ${\displaystyle a}$:

${\displaystyle x^{3}+{\frac {b}{a}}x^{2}+{\frac {c}{a}}x+{\frac {d}{a}}=0.}$

Abbiamo così portato il coefficiente di ${\displaystyle x^{3}}$ uguale ad 1. Ora dobbiamo annullare il termine di secondo grado, eseguendo una traslazione del tipo ${\displaystyle x=y-k}$ otteniamo:

${\displaystyle (y-k)^{3}+{\frac {b}{a}}(y-k)^{2}+{\frac {c}{a}}(y-k)+{\frac {d}{a}}=0.}$

Sviluppando le potenze di binomio si può notare che il coefficiente del termine di secondo grado è uguale a: ${\displaystyle (-3k+{\tfrac {b}{a}})}$ per annullarlo possiamo eguagliarlo a zero e ottenere:

${\displaystyle -3k+{\frac {b}{a}}=0\Longleftrightarrow k={\frac {b}{3a}}.}$

La sostituzione che dovremmo operare sarà quindi:

${\displaystyle x=y-{\frac {b}{3a}}.}$

Eseguendo i calcoli otteniamo un'equazione della forma:

${\displaystyle y^{3}+py+q=0,}$

ove:

${\displaystyle {\begin{cases}p=-{\frac {b^{2}}{3a^{2}}}+{\frac {c}{a}}\\q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}.\end{cases}}}$

Abbiamo così trasformato una classica equazione di terzo grado in un'equazione con termine di secondo grado nullo e coefficiente del termine di terzo grado uguale ad 1. Ora dobbiamo rendere del tutto identiche l'equazione appena ottenuta con l'equazione iniziale di cui conoscevamo la soluzione. Per fare ciò dobbiamo eguagliare i termini di primo grado ${\displaystyle -3uv}$ a ${\displaystyle p}$ e i termini noti ${\displaystyle -(u^{3}+v^{3})}$ a ${\displaystyle q}$ risolvendo il sistema:

${\displaystyle {\begin{cases}-3uv=p\\-(u^{3}+v^{3})=q\end{cases}}\Rightarrow {\begin{cases}uv=-{\frac {p}{3}}\\u^{3}+v^{3}=-q.\end{cases}}}$

Se eleviamo al cubo la prima equazione del sistema otteniamo:

${\displaystyle {\begin{cases}u^{3}v^{3}=-{\frac {p^{3}}{27}}\\u^{3}+v^{3}=-q.\end{cases}}}$

Il sistema ci chiede di trovare due incognite la cui somma è ${\displaystyle -q}$ e il prodotto è ${\displaystyle -{\frac {p^{3}}{27}}}$. Per risolvere un sistema del genere si può utilizzare l'equazione di secondo grado:

${\displaystyle z^{2}-rz+s=0,}$

ove ${\displaystyle r}$ e ${\displaystyle s}$ rappresentano rispettivamente la somma e il prodotto delle nostre due incognite, risolviamo quindi l'equazione:

${\displaystyle z^{2}+qz-{\frac {p^{3}}{27}}=0}$

${\displaystyle u^{3}={\frac {-q+{\sqrt {q^{2}+{\frac {4p^{3}}{27}}}}}{2}}=-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}\ \Rightarrow \ u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}}$

${\displaystyle v^{3}={\frac {-q-{\sqrt {q^{2}+{\frac {4p^{3}}{27}}}}}{2}}=-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}\ \Rightarrow \ v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Dato che la soluzione della nostra equazione è ${\displaystyle y=u+v}$ possiamo scrivere:

${\displaystyle y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$

Utilizzo dei numeri complessi per trovare le soluzioni dell'equazione

La formula risolutiva trovata presenta due radici cubiche che in campo reale hanno una sola soluzione ma in campo complesso ne hanno ben 3 ciascuna. Essa quindi fornisce in totale 9 risultati dei quali solo 3 di essi saranno una soluzione dell'equazione di terzo grado, questo perché il teorema fondamentale dell'algebra asserisce che un'equazione di grado ${\displaystyle n}$ ammette precisamente ${\displaystyle n}$ soluzioni.

Il problema deriva dal fatto che abbiamo elevato al cubo la prima equazione del sistema

${\displaystyle {\begin{cases}uv=-{\frac {p}{3}}\\u^{3}+v^{3}=-q\end{cases}}}$

e quindi, dato che stiamo ragionando in campo complesso, le soluzioni del precedente sistema sono quelle soluzioni di

${\displaystyle {\begin{cases}u^{3}v^{3}=-{\frac {p^{3}}{27}}\\u^{3}+v^{3}=-q\end{cases}}}$

che risolvono ${\displaystyle uv=-{\tfrac {p}{3}}}$ e in particolare dato che ${\displaystyle -{\tfrac {p}{3}}}$ è un numero reale dobbiamo verificare quando ${\displaystyle uv}$ è anch'esso reale.

È da notare inoltre che la formula risolutiva presenta anche delle radici quadrate che in campo complesso hanno sempre 2 soluzioni che dovremmo sempre prendere in considerazione.

Chiamiamo quindi ${\displaystyle {\tfrac {q^{2}}{4}}+{\tfrac {p^{3}}{27}}}$ con il simbolo ${\displaystyle \Delta _{\text{III}}}$ e studiamo i due casi: ${\displaystyle \Delta _{\text{III}}}$ positivo e ${\displaystyle \Delta _{\text{III}}}$ negativo e il caso speciale in cui ${\displaystyle \Delta _{\text{III}}}$ è nullo.

Caso: Δ_III<0

Possiamo riscrivere la formula risolutiva nel modo seguente:

${\displaystyle y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}}$

${\displaystyle y={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {-1(-\Delta _{\text{III}})}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {-1(-\Delta _{\text{III}})}}}}}$

${\displaystyle y={\sqrt[{3}]{-{\frac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}}}+{\sqrt[{3}]{-{\frac {q}{2}}-i{\sqrt {-\Delta _{\text{III}}}}}}}$

Per calcolare le radici cubiche possiamo convertire i numeri complessi ${\displaystyle -{\tfrac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}}$ e ${\displaystyle -{\tfrac {q}{2}}-i{\sqrt {-\Delta _{\text{III}}}}}$ in forma trigonometrica. I due moduli quindi saranno uguali a:

${\displaystyle \rho ={\sqrt {\left(-{\frac {q}{2}}\right)^{2}+{\big (}{\sqrt {-\Delta _{\text{III}}}}{\big )}^{2}}}={\sqrt {{\frac {q^{2}}{4}}-{\frac {q^{2}}{4}}-{\frac {p^{3}}{27}}}}={\sqrt {-{\frac {p^{3}}{27}}}}.}$

Gli angoli avranno la stessa ampiezza ma segno opposto dato che le parti immaginarie dei due numeri complessi sono opposte, li chiameremo quindi ${\displaystyle \theta }$ e ${\displaystyle -\theta }$.

Calcoliamo ora le radici cubiche dei numeri ${\displaystyle (\rho ,\theta )}$ e ${\displaystyle (\rho ,-\theta )}$. Il loro modulo è uguale a:

${\displaystyle {\sqrt[{3}]{\rho }}={\sqrt[{3}]{\sqrt {-{\frac {p^{3}}{27}}}}}={\sqrt[{3}]{\left({\sqrt {-{\frac {p}{3}}}}\right)^{3}}}={\sqrt {-{\frac {p}{3}}}}}$

e le radici saranno:

${\displaystyle {\sqrt[{3}]{-{\frac {q}{2}}+i{\sqrt {-\Delta _{\text{III}}}}}}={\begin{cases}{\sqrt {-{\frac {p}{3}}}}\left(\cos {\frac {\theta }{3}}+i\sin {\frac {\theta }{3}}\right)&(u_{1})\\{\sqrt {-{\frac {p}{3}}}}\left(\cos {\frac {\theta +2\pi }{3}}+i\sin {\frac {\theta +2\pi }{3}}\right)&(u_{2})\\{\sqrt {-{\frac {p}{3}}}}\left(\cos {\frac {\theta +4\pi }{3}}+i\sin {\frac {\theta +4\pi }{3}}\right)&(u_{3})\\\end{cases}}}$

${\displaystyle {\sqrt[{3}]{-{\frac {q}{2}}-i{\sqrt {-\Delta _{\text{III}}}}}}={\begin{cases}{\sqrt {-{\frac {p}{3}}}}\left(\cos {\frac {-\theta }{3}}+i\sin {\frac {-\theta }{3}}\right)&(v_{1})\\{\sqrt {-{\frac {p}{3}}}}\left(\cos {\frac {-\theta +2\pi }{3}}+i\sin {\frac {-\theta +2\pi }{3}}\right)&(v_{2})\\{\sqrt {-{\frac {p}{3}}}}\left(\cos {\frac {-\theta +4\pi }{3}}+i\sin {\frac {-\theta +4\pi }{3}}\right)&(v_{3})\\\end{cases}}}$

Le soluzioni saranno quindi della forma ${\displaystyle y=u_{i}+v_{j}}$ ma in realtà solo in tre casi il prodotto ${\displaystyle u_{i}v_{j}}$ ci restituisce un numero reale (e quindi risolve ${\displaystyle uv=-{\tfrac {p}{3}}}$). Infatti esclusivamente nei casi ${\displaystyle u_{1}v_{1}}$, ${\displaystyle u_{2}v_{3}}$ e ${\displaystyle u_{3}v_{2}}$ la parte immaginaria si annulla.

Quindi le soluzioni dell'equazione saranno:

${\displaystyle y_{1}=u_{1}+v_{1}=2{\sqrt {-{\frac {p}{3}}}}\cos {\frac {\theta }{3}};}$

${\displaystyle y_{2}=u_{2}+v_{3}=2{\sqrt {-{\frac {p}{3}}}}\cos {\frac {\theta +2\pi }{3}};}$

${\displaystyle y_{3}=u_{3}+v_{2}=2{\sqrt {-{\frac {p}{3}}}}\cos {\frac {\theta +4\pi }{3}}.}$

Caso: Δ_III>0

Nel caso in cui ${\displaystyle \Delta _{\text{III}}}$ sia maggiore di 0 esso avrà una radice quadrata reale e quindi esisteranno due numeri reali ${\displaystyle u_{1}}$ e ${\displaystyle v_{1}}$ uguali a

${\displaystyle u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}};}$

${\displaystyle v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}}.}$

Come nel caso precedente non bisogna soffermarsi sulle radici reali ma bisogna analizzare anche cosa avviene quando il risultato delle radici cubiche è complesso. Per trovare anche i risultati complessi basterà moltiplicare i risultati reali ${\displaystyle u_{1}}$ e ${\displaystyle v_{1}}$ per le radici cubiche dell'unità; abbiamo quindi i 6 risultati:

${\displaystyle u_{1}={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {\Delta _{\text{III}}}}}},\quad u_{2}=u_{1}\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad u_{3}=u_{1}\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right);}$

${\displaystyle v_{1}={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {\Delta _{\text{III}}}}}},\quad v_{2}=v_{1}\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right),\quad v_{3}=v_{1}\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right).}$

Anche questa volta, per controllare quando ${\displaystyle u_{i}v_{j}=-{\tfrac {p}{3}}}$, ci basta vedere quando ${\displaystyle u_{i}v_{j}}$ è un numero reale. Svolgendo i conti otteniamo quindi che le soluzioni dell'equazione di terzo grado sono:

${\displaystyle y_{1}=u_{1}+v_{1};}$

${\displaystyle y_{2}=u_{2}+v_{3}=u_{1}\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)+v_{1}\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right);}$

${\displaystyle y_{3}=u_{3}+v_{2}=u_{1}\left(-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)+v_{1}\left(-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right).}$

Caso: Δ_III=0

Nel caso particolare in cui ${\displaystyle \Delta _{\text{III}}}$ sia uguale a 0 si può ricavare dalle formule trovate che le soluzioni sono:

${\displaystyle y_{1}=-2{\sqrt[{3}]{\frac {q}{2}}};}$

${\displaystyle y_{2}=y_{3}={\sqrt[{3}]{\frac {q}{2}}}.}$

Soluzione in forma non depressa

Si consideri una generica cubica della forma:

${\displaystyle P(x)=ax^{3}+bx^{2}+cx+d=a(x-x_{1})(x-x_{2})(x-x_{3}).}$

Si calcolino

${\displaystyle q={\frac {3ac-b^{2}}{3a^{2}}}}$

${\displaystyle p={\frac {9abc-27a^{2}d-2b^{3}}{27a^{3}}}}$

${\displaystyle s={\sqrt[{3}]{{\frac {p}{2}}+{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}}$

${\displaystyle t={\sqrt[{3}]{{\frac {p}{2}}-{\sqrt {{\frac {q^{3}}{27}}+{\frac {p^{2}}{4}}}}}}.}$

Le soluzioni dell'equazione ${\displaystyle P(x)=0}$ sono date da:

${\displaystyle x_{1}=s+t-{\frac {b}{3a}};}$

${\displaystyle x_{2}=-{\frac {1}{2}}(s+t)-{\frac {b}{3a}}+{\frac {\sqrt {3}}{2}}(s-t)i;}$

${\displaystyle x_{3}=-{\frac {1}{2}}(s+t)-{\frac {b}{3a}}-{\frac {\sqrt {3}}{2}}(s-t)i.}$

Alternativamente, la soluzione generale dell'equazione di terzo grado in termini dei coefficienti può essere scritta in forma compatta nel seguente modo:

${\displaystyle x_{k}=-{\frac {b}{3a}}-{\frac {q}{3tu_{k}}}+tu_{k},\qquad k\in \{1,2,3\},}$

dove

${\displaystyle u_{1}=1\ ,\qquad u_{2}={-1-i{\sqrt {3}} \over 2},\qquad u_{3}={-1+i{\sqrt {3}} \over 2}}$

sono le tre radici cubiche dell'unità nel campo complesso. Essa può essere riscritta anche come

${\displaystyle x_{k}=-{\frac {1}{3a}}\left(b\ +\ u_{k}C\ +\ {\frac {\Delta _{0}}{u_{k}C}}\right),\qquad k\in \{1,2,3\},}$

dove

${\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}+{\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}}=-3at,}$

con

${\displaystyle \Delta _{0}=b^{2}-3ac=-3a^{2}q;}$

${\displaystyle \Delta _{1}=2b^{3}-9abc+27a^{2}d=-27a^{3}r.}$

Casi particolari

Caso 1: x³+x=c

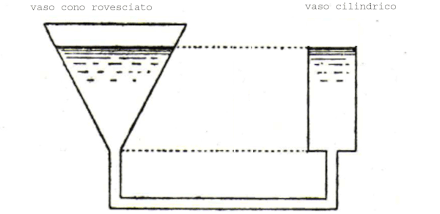
Un metodo di soluzione di tipo idraulico è stato trovato da A. Demanet nel 1898 e tratta il caso particolare^[5][6]

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

in cui ${\displaystyle a=1,b=0,c=1,d<0.}$ L'equazione può essere, quindi, riscritta in modo semplificato uguagliando ${\displaystyle k=-d}$

${\displaystyle x^{3}+x=k.}$

La soluzione si basa sulla teoria dei vasi comunicanti, mediante lo studio di un sistema formato da un vaso a cono rovesciato collegato ad uno cilindrico di eguale altezza, problemi di tensione superficiale possono rendere meno accurata la precisione della soluzione.

Ipotizziamo di avere il sistema descritto sopra, che l'area della base del cilindro sia uguale a 1 e che il rapporto tra il raggio ${\displaystyle r}$ del cono e la sua altezza ${\displaystyle a}$ sia:

${\displaystyle {\frac {r}{a}}={\sqrt {\frac {3}{\pi }}}.}$

Ora siano ${\displaystyle V_{\text{cono}}}$ e ${\displaystyle V_{\text{cilindro}}}$ rispettivamente il volume dell'acqua^[7] presente nel cono e nel cilindro, e sia ${\displaystyle h}$ l'altezza dell'acqua nei due recipienti^[8] si ha che:

${\displaystyle V_{\text{cilindro}}=h\cdot {\text{area}}_{\text{base}}=h\cdot 1=h,}$

e che

${\displaystyle V_{\text{cono}}=\pi r^{2}{\frac {h}{3}}.}$

Tenendo conto della relazione tra l'altezza e il raggio del cono si ha che:

${\displaystyle V_{\text{cono}}=\pi \left(h{\sqrt {\frac {3}{\pi }}}\right)^{2}{\frac {h}{3}}=h^{3}.}$

Sia ${\displaystyle V_{\text{tubo}}}$ il volume dell'acqua presente nel tubo che collega i due vasi e sia ${\displaystyle V_{\text{acqua}}}$ il volume dell'acqua versata nei due vasi si ha che:

${\displaystyle V_{\text{acqua}}=V_{\text{cilindro}}+V_{\text{cono}}+V_{\text{tubo}}}$

${\displaystyle V_{\text{acqua}}=h+h^{3}+V_{\text{tubo}}}$

${\displaystyle h^{3}+h=V_{\text{acqua}}-V_{\text{tubo}}.}$

Ponendo ${\displaystyle k=V_{\text{acqua}}-V_{\text{tubo}}}$, si ottiene:

${\displaystyle h^{3}+h=k.}$

Ottenendo così un'equazione di terzo grado la cui soluzione è l'altezza, misurabile, dell'acqua in uno dei due vasi comunicanti.

Più in generale, se si indicano con ${\displaystyle r_{\text{cono}}}$ e ${\displaystyle r_{\text{cilindro}}}$ rispettivamente il raggio del cono e del cilindro, con ${\displaystyle h}$ l'altezza del cono e con ${\displaystyle x}$ l'altezza raggiunta dall'acqua si può ottenere l'equazione:

${\displaystyle {\frac {1}{3}}\pi {\frac {(r_{\text{cono}})^{2}}{h^{2}}}x^{3}+\pi (r_{\text{cilindro}})^{2}x=k.}$

Quindi scegliendo opportunamente i due recipienti si può risolvere anche un'equazione del tipo:

${\displaystyle ax^{3}+bx=c,\qquad {\text{con }}c>0.}$

Caso 2: d=bc/a

Se l'equazione di terzo grado possiede la particolare caratteristica di avere il termine noto uguale a ${\displaystyle {\tfrac {bc}{a}}}$ l'equazione si presenta nella formula:

${\displaystyle ax^{3}+bx^{2}+cx+{\frac {bc}{a}}=0.}$

In questo caso si ha immediatamente almeno una soluzione reale dato che la formula può essere vista come:

${\displaystyle ax^{3}+bx^{2}+cx+{\frac {bc}{a}}=a\left(x+{\frac {b}{a}}\right)\left(x^{2}+{\frac {c}{a}}\right).}$

Una soluzione, quindi, è ${\displaystyle x=-{\tfrac {b}{a}}}$; le altre 2 saranno reali o no in base al segno di ${\displaystyle {\tfrac {c}{a}}}$.

Note

Bibliografia

• Carl Boyer, Storia della matematica, Milano, Arnoldo Mondadori Editore, 1976, ISBN 88-04-33431-2.

Voci correlate

• Funzione cubica
• Equazione lineare
• Equazione di secondo grado
• Equazione di quarto grado
• Teorema fondamentale dell'algebra
• Numero complesso

Altri progetti

• Wikimedia Commons contiene immagini o altri file su equazione di terzo grado

Collegamenti esterni

• (EN) cubic equation, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Equazione di terzo grado, su MathWorld, Wolfram Research.
• (EN) cubic formula, in PlanetMath.
• (EN) Cardano's derivation of the cubic formula, in PlanetMath.
• (EN) I.V. Proskuryakov, Cubic equation, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
• (EN) I.V. Proskuryakov, Cardano formula, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.

Controllo di autorità	Thesaurus BNCF 32448 · LCCN (EN) sh85044516 · BNF (FR) cb122693768 (data) · J9U (EN, HE) 987007552898505171