Gaya sentripetal

Bagian dari seri artikel mengenai
Mekanika klasik
${\displaystyle {\vec {F}}=m{\vec {a}}}$ Hukum kedua Newton
Sejarah Garis waktu
Cabang Benda langit Dinamika Kinematika Kinetika Kontinuum Statika Statistika Terapan
Dasar Asas D'Alembert Daya mekanik Energi kinetik potensial Gaya Impuls Inersia / Momen inersia Kecepatan Kelajuan Kerangka acuan Usaha mekanik Kerja maya Massa Momen Momentum Momentum sudut Pasangan Percepatan Ruang Torsi Waktu
Rumus padding-bottom:0.5em; Mekanika analisis Mekanika Lagrange Mekanika Hamilton Mekanika Routh Persamaan Hamilton–Jacobi Persamaan gerak Appell Persamaan Udwadia–Kalaba
Topik inti Benda tegar dinamika persamaan Euler Friksi Gaya fiksi Gerak (linear) Gerak harmonik sederhana Getaran Hukum gerak Euler Hukum gerak Newton Hukum gravitasi universal Newton Inersia / Kerangka acuan non-inersia Kecepatan relatif Mekanika gerak partikel planar Osilator harmonis Peredaman (rasio) Perpindahan Persamaan gerak
Rotasi Gerak melingkar Kerangka acuan berotasi Gaya sentripetal Gaya sentrifugal reaktif Gaya coriolis Pendulum Kecepatan tangensial Kecepatan putar Percepatan sudut / perpindahan / frekuensi / kecepatan
Ilmuwan Galileo Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
l b s

Gaya sentripetal atau gaya memusat adalah gaya yang membuat benda untuk bergerak melingkar. Gaya ini bukan merupakan gaya fisis, atau gaya dalam arti sebenarnya, melainkan hanya suatu penamaan atau penggolongan jenis-jenis gaya yang berfungsi membuat benda bergerak melingkar. Bermacam-macam gaya fisis dapat digunakan sebagai gaya sentripetal, antara lain gaya gravitasi, elektrostatik, tegangan tali, gesekan dan lainnya. Istilah sentripetal berasal dari kata bahasa Latin, yaitu centrum ("pusat") dan petere ("menuju arah"), yang berarti menuju arah pusat lingkaran.

Isaac Newton mendeskripsikannya gaya sentripetal sebagai "suatu gaya di mana benda ditarik atau didorong, atau dengan cara apa pun cenderung, menuju suatu titik sebagai pusat".^[1] Dalam mekanika Newton, gravitasi memberikan gaya sentripetal yang menyebabkan orbit astronomis.

Salah satu contoh umum yang melibatkan gaya sentripetal adalah kasus di mana benda bergerak dengan kecepatan seragam di sepanjang jalur melingkar. Gaya sentripetal diarahkan pada sudut siku-siku terhadap gerakan dan juga sepanjang jari-jari menuju pusat jalur melingkar.^[2][3] Deskripsi matematika diturunkan pada 1659 oleh fisikawan Belanda Christiaan Huygens.^[4]

Gagasan Newton tentang gaya sentripetal sesuai dengan apa yang sekarang disebut gaya pusat. Ketika satelit berada di orbit sekitar planet, gravitasi dianggap sebagai gaya sentripetal meskipun dalam kasus orbit eksentrik, gaya gravitasi diarahkan ke fokus, dan bukan ke pusat kelengkungan sesaat.^[5]

Rumus gaya sentripetal

Gaya sentripetal memiliki besar sebanding kuadrat kecepatan tangensial benda dan berbanding terbalik dengan jari-jari lintasan

${\displaystyle \!F_{s}=m{\frac {v^{2}}{r}}}$

dengan arah menuju pusat lintasan berbentuk lingkaran, yang menunjukkan bahwa terdapat suatu percepatan sentripetal, yaitu

${\displaystyle \!a_{s}={\frac {v^{2}}{r}}}$

apabila dianalogikan dengan hukum kedua Newton.

${\displaystyle \!F=ma}$

Representasi vektor

Dalam notasi vektor dengan sistem koordinat polar, gaya sentripetal dapat dituliskan sebagai

${\displaystyle \!{\vec {F_{s}}}=-m{\frac {v^{2}}{r}}{\hat {r}}}$

dengan

${\displaystyle \!{\hat {r}}={\frac {\vec {r}}{r}}}$

adalah vektor satuan dalam arah radial, yang umumnya dipilih bernilai positif mengarah ke luar lingkaran.

Representasi produk perkalian vektor

Atau dapat pula dituliskan sebagai produk dari perkalian vektor

${\displaystyle {\vec {F}}_{s}=-{\frac {mv^{2}}{r}}{\hat {r}}=-{\frac {mv^{2}}{r}}{\frac {\vec {r}}{r}}=-m\omega ^{2}{\vec {r}}=m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})}$

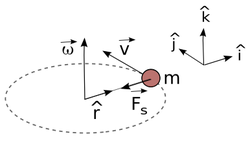
Dengan arah ${\displaystyle {\vec {\omega }}}$ mengikuti aturan tangan kanan. Dalam kasus seperti ditunjukkan dalam gambar, besaran-besaran vektor yang dimaksud bernilai:

${\displaystyle \!{\vec {\omega }}=\omega \ {\hat {k}}}$

${\displaystyle \!{\vec {r}}=r\left[\cos(\omega t)\ {\hat {i}}+\sin(\omega t)\ {\hat {j}}\right]}$

dan sebagai konsekuensinya

${\displaystyle \!{\hat {r}}=\cos(\omega t)\ {\hat {i}}+\sin(\omega t)\ {\hat {j}}}$

${\displaystyle \!{\vec {v}}={\vec {\omega }}\times {\vec {r}}=\omega r\ \left[-\sin(\omega t)\ {\hat {i}}+\cos(\omega t)\ {\hat {j}}\right]}$

Dengan demikian dapat dibuktikan bahwa

${\displaystyle {\vec {F}}_{s}=m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})=m{\vec {\omega }}\times {\vec {v}}}$

${\displaystyle =m(\omega {\hat {k}})\times \left(\omega r\ \left[-\sin(\omega t)\ {\hat {i}}+\cos(\omega t)\ {\hat {j}}\right]\right)}$

${\displaystyle =m\omega ^{2}r\left[-\sin(\omega t)\ {\hat {j}}-\cos(\omega t)\ {\hat {i}}\right]}$

${\displaystyle =m\omega ^{2}r\left\{-\left[\sin(\omega t)\ {\hat {j}}+\cos(\omega t)\ {\hat {i}}\right]\right\}}$

${\displaystyle =m\omega ^{2}r(-{\hat {r}})=-m\omega ^{2}{\vec {r}}}$

seperti dituliskan sebelumnya, yang menunjukkan bahwa gaya sentripetal selalu menuju ke pusat lintasan lingkaran.

Lihat pula

• hukum Newton
• perkalian vektor

Pranala luar

• (Indonesia) Gaya sentripetal Diarsipkan 2010-03-05 di Wayback Machine.

1. ^ Newton, Isaac, 1642-1727. (2010). The principia : mathematical principles of natural philosophy. [Place of publication not identified]: Snowball Pub. ISBN 978-1-60796-240-3. OCLC 701563361. Pemeliharaan CS1: Banyak nama: authors list (link)
2. ^ Hibbeler, R. C. (2010). Engineering mechanics. Dynamics (edisi ke-12th ed). Upper Saddle River, NJ: Prentice Hall. ISBN 978-0-13-607791-6. OCLC 356369748. Pemeliharaan CS1: Teks tambahan (link)
3. ^ Tipler, Paul Allen, 1933- ((2003 printing)). Physics for scientists and engineers. Mosca, Gene. (edisi ke-5th ed., extended). New York: W.H. Freeman. ISBN 0-7167-4389-2. OCLC 51095685. Diarsipkan dari versi asli tanggal 2008-12-07. Diakses tanggal 2020-10-09.  Periksa nilai tanggal di: |date= (bantuan)Pemeliharaan CS1: Banyak nama: authors list (link)
4. ^ Theoretical and applied mechanics : proceedings of the XVIIth International Congress of Theoretical and Applied Mechanics, held in Grenoble, France, 21-27 August, 1988. Germain, Paul, 1920-, Piau, Monique., Caillerie, Denis., International Union of Theoretical and Applied Mechanics. Amsterdam: North-Holland. 1989. ISBN 978-0-444-60020-2. OCLC 700400693. Diarsipkan dari versi asli tanggal 2023-07-29. Diakses tanggal 2020-10-09. 
5. ^ Koupelis, Theo (2010-02-04). In Quest of the Universe (dalam bahasa Inggris). Jones & Bartlett Learning. ISBN 978-0-7637-6858-4. Diarsipkan dari versi asli tanggal 2023-07-29. Diakses tanggal 2020-10-09.