Aszimptota

Az aszimptota a matematikában egy olyan görbét, többnyire egyenest jelent, amelyet egy függvény grafikonja határértékben megközelít, de nem éri el. Az aszimptota fogalma nem egységes: egyaránt beszélnek görbék és függvények aszimptotáiról.

Az aszimptota ἀσύμπτωτος görög eredetű, eredeti jelentése: nem egybeeső, nem egyező. Alapigéje συμπίπτειν, egybeesni, megegyezni, σύν (szün) együtt, egyszerre, πίπτειν esni.

Görbe aszimptotája

A görbék az n dimenziós tér, többnyire az euklideszi sík egydimenziós részhalmazai. Matematikai definíciójuk szerint ezek a görbék utak, legfeljebb megszámlálható sok helyen szakadó függvények, algebrai görbék grafikonjai. Ha egy grafikon hozzásimul egy egyeneshez, akkor az az egyenes a görbe aszimptotája.

Az e egyenes aszimptotája a γ görbének, ha a végtelenben tetszőlegesen megközelíti. Ez pontosabban azt jelenti, hogy ha egy P pont végigfut az e egyenesen, akkor P γ-tól mért távolsága a nullához tart. Formálisan:

${\displaystyle \lim _{P\in e,|P|\to \infty }d(P,\gamma )=0}$

ahol P és γ távolsága a P és a γ pontjai közötti távolságok infimuma:

${\displaystyle d(P,\gamma ):=\inf _{Q\in \gamma }d(P,Q)}$

Algebrai görbe aszimptotája a projektív szemlélet szerint a következőképpen értelmezhető:

Az aszimptota a végtelenben vett érintő.

Függvény aszimptotája

A függvény aszimptotája egy olyan grafikon, többnyire egyenes, ami a függvény grafikonját tetszőlegesen megközelíti. A függvény elemzése közben ki kell térni az aszimptotákra is.

Rendszerint olyan függvények aszimptotáit keresik, ahol a függvény a valós számok egy részhalmazából a valós számok halmazába képez.

Az aszimptotáknak két típusuk van aszerint, hogy a függvény az x vagy az y tengely irányában közeledik-e hozzá.

Közeledés az y tengely irányába

Ha az f függvénynek pólusa van t-ben, vagyis

${\displaystyle \lim _{x\nearrow t}f(x)=\pm \infty \,\,}$ vagy ${\displaystyle \,\,\lim _{x\searrow t}f(x)=\pm \infty ,}$

akkor x = t az f függvény függőleges aszimptotája.

Közeledés az x tengely irányába

Ha f, mint x függvénye a valós h számhoz tart a végtelenben, formálisan

${\displaystyle \lim _{x\to \infty }f(x)=h}$,

akkor az y = h egyenes f vízszintes aszimptotája. Hasonló teljesül, ha ${\displaystyle x\to -\infty }$.

Ha a p: R → R egyenes határértékben megközelíti az f függvényt, azaz

${\displaystyle \lim _{x\to \infty }[f(x)-p(x)]=0}$ vagy ${\displaystyle \lim _{x\to -\infty }[f(x)-p(x)]=0,}$

akkor p f ferde aszimptotája.

Ez a háromféle aszimptota együttesen megfelel a görbék aszimptotájának.

A ferde aszimptota fogalmát sokszor általánosítják, az egyenesek mellett még más közelítőgörbéket is megengedve. Így tekintenek polinomgörbéket aszimptotáknak. Ha f = g/h algebrai törtfüggvény, akkor f-nek mindig van ilyen értelemben vett aszimptotája: az a polinom, ami a g/h osztáskor keletkezik. Az aszimptotától mért függőleges távolság változását a valódi törtlineáris rész adja meg. Emellett y = 0 vízszintes aszimptota.

A polinomokon kívül más függvények is tekinthetők aszimptotának, feltéve, ha kielégítik a határérték-feltételt. Alkalmazás szempontjából hol az egyik, hol a másik hasznosabb.

Példák

Az

${\displaystyle f_{1}(x)={\frac {1}{x}}}$

függvénynek (lásd hiperbola) pólushelye, azaz függőleges aszimptotája van x = 0-ban, és van y = 0 vízszintes aszimptotája is.

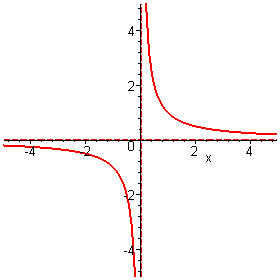
Az

${\displaystyle f_{2}(x)={\frac {x^{3}-x^{2}+5}{5x-5}}={\frac {x^{3}-x^{2}}{5x-5}}+{\frac {1}{x-1}}={\frac {1}{5}}x^{2}+{\frac {1}{x-1}}}$

függvénynek pólusa van x = 1 -ben, és (ha polinomok is megengedettek), akkor ${\displaystyle p(x)={\frac {1}{5}}x^{2}}$ közelítő parabolája.

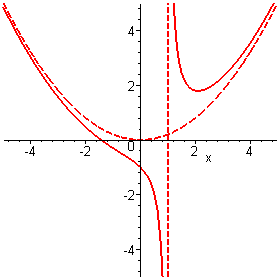
Források

• Aszimptota a Planetmath-nál
• Kuptsov, L.P. (2001), "Asymptote", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104