Sphère de Riemann

Pour les articles homonymes, voir Sphère (homonymie).

Cet article ne cite pas suffisamment ses sources (décembre 2023).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l'infini, de manière que certaines expressions mathématiques deviennent convergentes et élégantes, du moins dans certains contextes. Déjà envisagée par le mathématicien Carl Friedrich Gauss, elle est baptisée du nom de son élève Bernhard Riemann. Ce plan s'appelle également la droite projective complexe, dénoté ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$.

Introduction

La sphère de Riemann, obtenue en ajoutant au plan complexe un point à l'infini, est une variété complexe unidimensionnelle, également appelée une surface de Riemann.

En analyse complexe, la sphère de Riemann permet une expression élégante de la théorie des fonctions méromorphes. La sphère de Riemann est omniprésente en géométrie projective et en géométrie algébrique comme exemple fondamental d'une variété complexe, d'un espace projectif, et d'une variété algébrique. Elle a également une utilité dans d'autres disciplines qui dépendent de l'analyse et de la géométrie, telle que la physique quantique (représentation des états quantiques) et d'autres branches de la physique (théorie des twisteurs par exemple).

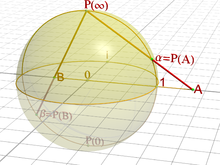
La projection stéréographique, par exemple sur le plan équatorial à partir du pôle Nord, permet de voir que la sphère est homéomorphe au plan complété du point à l'infini ${\displaystyle {\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$. Inversement, on passe du plan à la sphère en ajoutant un pôle, projection du point à l'infini noté ${\displaystyle P(\infty )}$. Le plan ${\displaystyle \mathbb {R} ^{2}}$ s'identifie à ${\displaystyle \mathbb {C} }$.

La sphère de Riemann, c'est la sphère usuelle envisagée de ce point de vue, autrement dit la droite projective complexe.

Le théorème d'uniformisation assure que c'est l'unique variété complexe de dimension 1 compacte et simplement connexe.

Remarque

Plus généralement, l'espace ${\displaystyle \mathbb {R} ^{n}}$ est homéomorphe à la sphère ${\displaystyle S^{n}}$ (sphère unité de l'espace euclidien ${\displaystyle \mathbb {R} ^{n+1}}$) privée d'un point. En effet, ${\displaystyle S^{n}}$ est le compactifié d'Alexandrov de ${\displaystyle \mathbb {R} ^{n}}$.

La droite projective complexe

C'est l'ensemble des droites vectorielles de ${\displaystyle \mathbb {C} ^{2}\,}$. Une telle droite étant définie par un vecteur non nul, défini à un coefficient de proportionnalité près, on peut la voir comme ${\displaystyle \mathbb {C} ^{2}\setminus \{0\}\,}$ quotienté par la relation d'équivalence

On la note ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$, et on note ${\displaystyle [z,t]\,}$ le point associé à ${\displaystyle (z,t)\,}$. On dit que ${\displaystyle (z,t)\,}$ est un système de coordonnées homogènes du point ${\displaystyle [z,t]\,}$.

Remarquons aussi que ${\displaystyle \phi _{1}:z\mapsto [z,1]}$ est une bijection de ${\displaystyle \mathbb {C} }$ sur ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )\setminus [1,0]}$.
De même : ${\displaystyle \phi _{2}:z\mapsto [1,z]}$ est une bijection de ${\displaystyle \mathbb {C} }$ sur ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )\setminus [0,1]}$.

Ces deux façons d'identifier ${\displaystyle \mathbb {C} }$ à ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$ privé d'un point sont analogues aux identifications de ${\displaystyle \mathbb {R} ^{2}\,}$ à la sphère unité privée d'un point à l'aide des projections stéréographiques de pôles Nord et Sud.

Cette remarque permet de donner une bijection explicite entre ${\displaystyle S^{2}={\big \{}(X,Y,Z)\in \mathbb {R} ^{3}\,{\big |}\,X^{2}+Y^{2}+Z^{2}=1{\big \}}}$ et ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$. C'est l'application ${\displaystyle g\,}$ définie par

${\displaystyle g(X,Y,Z)=[X+iY,1-Z]\,}$ si ${\displaystyle Z\not =1\,}$ et ${\displaystyle g(X,Y,Z)=[1+Z,X-iY]\,}$ si ${\displaystyle Z\not =-1\,}$

(ces deux définitions sont compatibles si ${\displaystyle Z\not =\pm 1}$, grâce à l'équation de la sphère).

Son application réciproque, si on identifie ${\displaystyle \mathbb {R} ^{3}}$ à ${\displaystyle \mathbb {C} \times \mathbb {R} }$, et si on représente un point de ${\displaystyle \mathbb {P} ^{1}(\mathbb {C} )}$ par des coordonnées homogènes, est

${\displaystyle H:(z,t)\mapsto \left({\frac {2z{\overline {t}}}{\vert z\vert ^{2}+\vert t\vert ^{2}}},{\frac {\vert z\vert ^{2}-\vert t\vert ^{2}}{\vert z\vert ^{2}+\vert t\vert ^{2}}}\right)}$

Il est clair que ${\displaystyle H(z,t)}$ ne dépend pas du choix des coordonnées homogènes. On peut aussi voir ${\displaystyle H}$ comme une application de

${\displaystyle S^{3}=\{(z,t)\in \mathbb {C} ^{2},\vert z\vert ^{2}+\vert t\vert ^{2}=1\}}$

On obtient alors la fibration de Hopf.

Homographies

On peut faire agir ${\displaystyle GL_{2}(\mathbb {C} )}$ sur la sphère par transformations de Möbius ; la matrice ${\displaystyle {\begin{pmatrix}a&b\\c&d\\\end{pmatrix}}}$ agit sur ${\displaystyle z\in \mathbb {P} ^{1}(\mathbb {C} )}$ ainsi :

• si ${\displaystyle z\in \mathbb {C} }$ et ${\displaystyle cz+d\neq 0}$, on lui associe ${\displaystyle {\frac {az+b}{cz+d}}}$ ;
• si ${\displaystyle z\in \mathbb {C} }$ et ${\displaystyle cz+d=0}$, on lui associe ${\displaystyle \infty }$ ;
• si ${\displaystyle z=\infty }$ et ${\displaystyle c=0}$, on lui associe ${\displaystyle \infty }$ ;
• si ${\displaystyle z=\infty }$ et ${\displaystyle c\neq 0}$, on lui associe ${\displaystyle {\frac {a}{c}}}$ .

En fait, on obtient ainsi une action à gauche du groupe projectif ${\displaystyle PGl(2,\mathbb {C} )}$.

L'application de la sphère de Riemann dans elle-même ainsi définie s'appelle une homographie ; c'est une bijection holomorphe ; inversement, toute bijection holomorphe de la sphère de Riemann est une homographie.

Voir aussi

• Résidu à l'infini
• Carte locale
• Fibration de Hopf

• Portail des mathématiques