En matemáticas , el coseno es una función par y continua con periodo 2 π {\displaystyle 2\pi } función trascendente . Su nombre se abrevia cos .
cos x = cos ( − x ) {\displaystyle \cos \;x=\cos(-x)} cos x = − cos ( x + π ) {\displaystyle \cos \;x=-\cos(x+\pi )} En trigonometría, el coseno de un ángulo α {\displaystyle \alpha } triángulo rectángulo se define como la razón entre el cateto adyacente a dicho ángulo y la hipotenusa:
cos α = b c = A C A B {\displaystyle \cos \alpha ={\frac {b}{c}}={\frac {AC}{AB}}} Esta razón no depende del tamaño del triángulo rectángulo escogido sino que es una función dependiente del ángulo α . {\displaystyle \alpha .}
Si B {\displaystyle B} O = A {\displaystyle O=A}
cos α = b = A C {\displaystyle \cos \alpha =b=AC} Ya que c = A B = 1 {\displaystyle c=AB=1}
Esta construcción permite representar el valor del coseno para ángulos no agudos y funciona exactamente igual para los vectores, representando un vector A B → {\displaystyle {\vec {AB}}} A C → {\displaystyle {\vec {AC}}} C B → {\displaystyle {\vec {CB}}}
Cálculo por serie de potencias En análisis matemático el coseno es la función que asocia un número real x {\displaystyle x} radianes , x {\displaystyle x} función trascendente y analítica , cuya expresión en serie de potencias es:
cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + … + ( − 1 ) n x 2 n ( 2 n ) ! + … {\displaystyle \cos x=1-{\cfrac {x^{2}}{2!}}+{\cfrac {x^{4}}{4!}}-{\cfrac {x^{6}}{6!}}+\ldots +(-1)^{n}\;{\frac {x^{2n}}{(2n)!}}+\ldots } que en sumatorio sería:
cos x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! {\displaystyle \cos x=\sum _{n=0}^{\infty }\;(-1)^{n}\;{\frac {x^{2n}}{(2n)!}}} En el plano complejo En el plano complejo a través de la fórmula de Euler se tiene que:
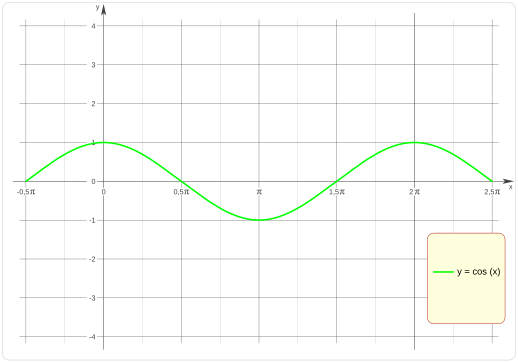
Representación gráfica Gráfica de la función coseno, con el eje X expresado en radianes. Relaciones trigonométricas El coseno puede relacionarse con otras funciones trigonométricas mediante el uso de identidades trigonométricas .
cos α = cos ( α + k 2 π ) , k ∈ Z {\displaystyle \cos \;\alpha =\;\;\;\cos \;(\alpha +k2\pi ),\;\;k\in \mathbb {Z} } Por inducción ya que aplicando un número par de veces cos α = − cos ( α + π ) {\displaystyle \cos \;\alpha =-\cos(\alpha +\pi )}
Relación entre el seno y el coseno La curva del coseno es la curva del seno desplazada π 2 {\displaystyle {\frac {\pi }{2}}}
cos α = sen ( α + π 2 ) {\displaystyle \cos \alpha =\operatorname {sen} \left(\alpha +{\frac {\pi }{2}}\right)} Coseno de la suma de dos ángulos Coseno del ángulo doble Coseno del ángulo mitad cos ( α 2 ) = { 1 + cos α 2 si α 2 ∈ [ − π 2 , π 2 ) + 2 k π − 1 + cos α 2 si α 2 ∈ [ π 2 , 3 π 2 ) + 2 k π , p a r a k ∈ Z {\displaystyle \cos {\bigg (}{\frac {\alpha }{2}}{\bigg )}={\begin{cases}{\sqrt {\frac {1+\cos \alpha }{2}}}&{\text{ si }}{\frac {\alpha }{2}}\in [-{\frac {\pi }{2}},\,\,{\frac {\pi }{2}}\,)+2k\pi \\-{\sqrt {\frac {1+\cos \alpha }{2}}}&{\text{ si }}{\frac {\alpha }{2}}\in [\;\;\;{\frac {\pi }{2}},\,{\frac {3\pi }{2}})+2k\pi \end{cases}}\;,\;\;para\;k\in \mathbb {Z} } Usando las fórmulas: sen 2 θ + cos 2 θ = 1 {\displaystyle \operatorname {sen} ^{2}\theta +\cos ^{2}\theta =1\,} cos ( 2 θ ) = cos 2 θ − sen 2 θ {\displaystyle \cos \left(2\theta \right)=\cos ^{2}\theta -\operatorname {sen} ^{2}\theta } resulta:
cos ( 2 θ ) = 2 cos 2 θ − 1 {\displaystyle \cos \left(2\theta \right)=2\cos ^{2}\theta -1} Representación de y = 1 + cos ( 2 x ) 2 . {\displaystyle y\;=\;{\sqrt {\frac {1+\cos(2x)}{2}}}.} y aislando sen θ {\displaystyle \operatorname {sen} \theta }
| cos θ | = 1 + cos ( 2 θ ) 2 {\displaystyle \vert \cos \theta \vert ={\sqrt {\frac {1+\cos(2\theta )}{2}}}} El cambio θ = α 2 {\displaystyle \theta ={\frac {\alpha }{2}}}
0 < cos α 2 si α 2 ∈ [ − π 2 , π 2 ) + 2 k π , {\displaystyle 0<\cos {\frac {\alpha }{2}}\;\;\;\;\;{\text{si}}\;\;\;{\frac {\alpha }{2}}\in [-{\frac {\pi }{2}},\,{\frac {\pi }{2}})+2k\pi ,} 0 > cos α 2 si α 2 ∈ [ π 2 , 3 π 2 ) + 2 k π {\displaystyle 0>\cos {\frac {\alpha }{2}}\;\;\;\;\;{\text{si}}\;\;\;{\frac {\alpha }{2}}\in [{\frac {\pi }{2}},\,{\frac {3\pi }{2}})+2k\pi } donde k ∈ Z {\displaystyle k\in \mathbb {Z} }
Suma de funciones como producto cos a + cos b = 2 cos ( a + b 2 ) cos ( a − b 2 ) {\displaystyle \cos a+\cos b=\;\;\;2\cos \left({\frac {a+b}{2}}\right)\cos \left({\frac {a-b}{2}}\right)} cos a − cos b = − 2 sen ( a + b 2 ) sen ( a − b 2 ) {\displaystyle \cos a-\cos b=-2\operatorname {sen} \left({\frac {a+b}{2}}\right)\operatorname {sen} \left({\frac {a-b}{2}}\right)}
La demostración está en la sección de identidades trigonométricas .
Producto de funciones como suma cos ( A ) cos ( B ) = cos 2 ( A + B 2 ) − sen 2 ( A − B 2 ) = cos 2 ( A − B 2 ) − sen 2 ( A + B 2 ) {\displaystyle \cos(A)\cos(B)=\cos ^{2}\left({\frac {A+B}{2}}\right)-\;\operatorname {sen} ^{2}\left({\frac {A-B}{2}}\right)=\cos ^{2}\left({\frac {A-B}{2}}\right)-\;\operatorname {sen} ^{2}\left({\frac {A+B}{2}}\right)} cos ( A ) cos ( B ) = 1 2 ( cos ( A + B ) + cos ( A − B ) ) {\displaystyle \cos(A)\cos(B)={\frac {1}{2}}\left(\cos(A+B)+\cos(A-B)\right)} Ángulos para los cuales el coseno se conoce con exactitud Ángulos en Rad (X) Ángulos en Grados (X°) Cos(X) π 6 {\displaystyle {\frac {\pi }{6}}} 30° 3 2 {\displaystyle {\frac {\sqrt {3}}{2}}} π 4 {\displaystyle {\frac {\pi }{4}}} 45° 2 2 {\displaystyle {\frac {\sqrt {2}}{2}}} π 3 {\displaystyle {\frac {\pi }{3}}} 60° 1 2 {\displaystyle {\frac {1}{2}}} π 2 {\displaystyle {\frac {\pi }{2}}} 90° 0 {\displaystyle 0} π {\displaystyle \pi } 180° − 1 {\displaystyle -1} 2 π {\displaystyle 2\pi } 360° 1 {\displaystyle 1}
Tomando los mismos valores para los ángulos con signo opuesto a los ángulos enunciados en la tabla, puesto que el coseno es una función par .
Derivada del coseno cos ′ x = − sen x {\displaystyle \cos 'x=-\operatorname {sen} x\,} Generalizaciones del coseno Véase también Enlaces externos
Q1256164 Cosine function / Q1256164 


 Datos: Q1256164
Datos: Q1256164 Multimedia: Cosine function / Q1256164
Multimedia: Cosine function / Q1256164







































































