Castigliano's method

Theorems describing elastic materials

Castigliano's method, named after Carlo Alberto Castigliano, is a method for determining the displacements of a linear-elastic system based on the partial derivatives of the energy. He is known for his two theorems. The basic concept may be easy to understand by recalling that a change in energy is equal to the causing force times the resulting displacement. Therefore, the causing force is equal to the change in energy divided by the resulting displacement. Alternatively, the resulting displacement is equal to the change in energy divided by the causing force. Partial derivatives are needed to relate causing forces and resulting displacements to the change in energy.

  • Castigliano's first theorem – for forces in an elastic structure

    Castigliano's method for calculating forces is an application of his first theorem, which states:

    If the strain energy of an elastic structure can be expressed as a function of generalised displacement qi then the partial derivative of the strain energy with respect to generalised displacement gives the generalised force Qi.

    In equation form,

    Q i = ∂ U ∂ q i {\displaystyle Q_{i}={\frac {\partial U}{\partial q_{i}}}}
    where U is the strain energy.

    If the force-displacement curve is nonlinear then the complementary strain energy needs to be used instead of strain energy. [1]
  • Castigliano's second theorem – for displacements in a linearly elastic structure.

    Castigliano's method for calculating displacements is an application of his second theorem, which states:

    If the strain energy of a linearly elastic structure can be expressed as a function of generalised force Qi then the partial derivative of the strain energy with respect to generalised force gives the generalised displacement qi in the direction of Qi.

    As above this can also be expressed as:

    q i = ∂ U ∂ Q i . {\displaystyle q_{i}={\frac {\partial U}{\partial Q_{i}}}.}

Examples

For a thin, straight cantilever beam with a load P at the end, the displacement δ {\displaystyle \delta } at the end can be found by Castigliano's second theorem :

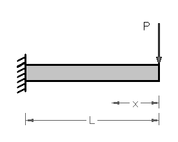
Cantilever Beam
Cantilever Beam with a Point Load at Free End

δ = ∂ U ∂ P {\displaystyle \delta ={\frac {\partial U}{\partial P}}}
δ = ∂ ∂ P ∫ 0 L M 2 ( x ) 2 E I d x = ∂ ∂ P ∫ 0 L ( P x ) 2 2 E I d x {\displaystyle \delta ={\frac {\partial }{\partial P}}\int _{0}^{L}{{\frac {M^{2}(x)}{2EI}}dx}={\frac {\partial }{\partial P}}\int _{0}^{L}{{\frac {(Px)^{2}}{2EI}}dx}}
where E {\displaystyle E} is Young's modulus, I {\displaystyle I} is the second moment of area of the cross-section, and M ( x ) = P x {\displaystyle M(x)=Px} is the expression for the internal moment at a point at distance x {\displaystyle x} from the end. The integral evaluates to:
δ = ∫ 0 L P x 2 E I d x = P L 3 3 E I . {\displaystyle {\begin{aligned}\delta &=\int _{0}^{L}{{\frac {Px^{2}}{EI}}dx}\\&={\frac {PL^{3}}{3EI}}.\end{aligned}}}

The result is the standard formula given for cantilever beams under end loads.

Castigliano's theorems apply if the strain energy is finite. This is true if m − i > n / 2 {\displaystyle m-i>n/2} .[2] It is m = 1 , 2 {\displaystyle m=1,2} the order of the energy (= the highest derivative in the energy), i = 0 , 1 , 2 , 3 {\displaystyle i=0,1,2,3} , is the index of the Dirac delta (single force, i = 0 {\displaystyle i=0} ) and n = 1 , 2 , 3 {\displaystyle n=1,2,3} is the dimension of the space. To second order equations, m = 1 {\displaystyle m=1} , belong two Dirac deltas, i = 0 {\displaystyle i=0} , force and i = 1 {\displaystyle i=1} , dislocation and to fourth order equations, m = 2 {\displaystyle m=2} , four Dirac deltas, i = 0 {\displaystyle i=0} force, i = 1 {\displaystyle i=1} moment, i = 2 {\displaystyle i=2} bend, i = 3 {\displaystyle i=3} dislocation.

Example: If a plate, m = 1 , n = 2 {\displaystyle m=1,n=2} , is loaded with a single force, i = 0 {\displaystyle i=0} , the inequality is not valid, 1 − 0 ≯ 2 / 2 {\displaystyle 1-0\ngtr 2/2} , also not in 3 − D {\displaystyle 3-D} , m = 1 , n = 3 , 1 − 0 ≯ 3 / 2 {\displaystyle m=1,n=3,1-0\ngtr 3/2} . Nor does it apply to a membrane (Laplace), m = 1 , n = 2 , i = 0 {\displaystyle m=1,n=2,i=0} , or a Reissner-Mindlin plate, m = 1 , n = 2 , i = 0 {\displaystyle m=1,n=2,i=0} . In general Castigliano's theorems do not apply to 2 − D {\displaystyle 2-D} and 3 − D {\displaystyle 3-D} problems. The exception is the Kirchhoff plate, m = 2 , n = 2 , i = 0 {\displaystyle m=2,n=2,i=0} , since 2 − 0 > 2 / 2 {\displaystyle 2-0>2/2} . But a moment, i = 1 {\displaystyle i=1} , causes the energy of a Kirchhoff plate to overflow, 2 − 1 ≯ 2 / 2 {\displaystyle 2-1\ngtr 2/2} . In 1 − D {\displaystyle 1-D} problems the strain energy is finite if m − i > 1 / 2 {\displaystyle m-i>1/2} .

Menabrea's theorem is subject to the same restriction. It needs that m − i > n / {\displaystyle m-i>n/} 2 is valid. It is i {\displaystyle i} the order of the support reaction, single force i = 0 {\displaystyle i=0} , moment i = 1 {\displaystyle i=1} . Except for a Kirchhoff plate and i = 0 {\displaystyle i=0} (single force as support reaction), it is generally not valid in 2 − D {\displaystyle 2-D} and 3 − D {\displaystyle 3-D} because the presence of point supports results in infinitely large energy.

External links

  • Carlo Alberto Castigliano
  • Castigliano's method: some examples(in German)

References

  1. ^ History of Strength of Materials, Stephen P. Timoshenko, 1993, Dover Publications, New York
  2. ^ Statics and Influence Functions from a Modern Perspective, Hartmann, Jahn, Chapter 1.35 Sobolev's Embedding Theorem, 2nd ed. 2021, Springer, p. 71
  • v
  • t
  • e
Structural engineering
Dynamic analysis
  • Duhamel's integral
  • Modal analysis
Static analysis
Structural elements
1-dimensional
2-dimensional
Structural support
  • Bracket
Theories
  • Category