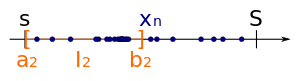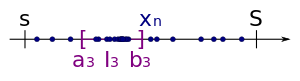Satz von Bolzano-Weierstraß
Der Satz von Bolzano-Weierstraß (nach Bernard Bolzano und Karl Weierstraß) ist ein Satz der Analysis über die Existenz konvergenter Teilfolgen.
Formulierungen des Satzes von Bolzano-Weierstraß
Für den Satz von Bolzano-Weierstraß gibt es folgende Formulierungen, die alle äquivalent zueinander sind:
- Jede beschränkte Folge komplexer Zahlen (mit unendlich vielen Gliedern) enthält (mindestens) eine konvergente Teilfolge.
- Jede beschränkte Folge komplexer Zahlen (mit unendlich vielen Gliedern) hat (mindestens) einen Häufungspunkt.
- Jede beschränkte Folge reeller Zahlen hat (mindestens) einen Häufungspunkt.
Beweisskizze
Der Beweis der allgemeinen Aussagen wird auf die eindimensionale reelle Aussage zurückgeführt. Diese kann man beweisen, indem man gleichzeitig eine Intervallschachtelung und eine Teilfolge konstruiert, so dass für jedes gilt . Diese zwei Folgen werden rekursiv konstruiert.
- Als Startpunkt dient das Intervall , wobei L eine Schranke der Folge ist, d. h. alle Folgeglieder sind im Intervall enthalten. Weiter kann als erstes Glied der zu bestimmenden Teilfolge gesetzt werden.
- Im Schritt von k zu k+1 enthält das Intervall unendlich viele Folgeglieder.
- Zuerst wird das Intervall halbiert in und mit dem Mittelpunkt .
- Es können nicht in beiden Teilintervallen nur endlich viele Folgeglieder liegen. Es kann also immer ein Teilintervall mit unendlich vielen Folgenglieder ausgewählt werden, diese Hälfte wird mit bezeichnet.
- Schließlich wird das nächste Glied der Teilfolge als das erste Element bestimmt, das in liegt und dessen Index größer ist als der des zuvor gewählten Elements, .
- Der Rekursionsschritt wird für alle durchgeführt. Das betrachtete Intervall wird dabei immer kleiner, , die Länge konvergiert gegen Null, wie es von einer Intervallschachtelung verlangt wird. Nach der Konstruktion ist der gemeinsame Punkt aller Intervalle , auch schon der Grenzwert der Teilfolge, , und damit ein Häufungspunkt der vorgegebenen beschränkten Folge.
Um den größten Häufungspunkt zu bestimmen, muss man, wann immer möglich, das obere Teilintervall wählen, für den kleinsten Häufungspunkt das untere Teilintervall.
Der Beweis beruht entscheidend auf dem Intervallschachtelungsprinzip, welches wiederum äquivalent ist zur Vollständigkeit der reellen Zahlen.
Visualisierung der Beweisskizze
-
 Gegeben sei eine beschränkte Folge . Diese besitzt damit eine untere Schranke und eine obere Schranke .
Gegeben sei eine beschränkte Folge . Diese besitzt damit eine untere Schranke und eine obere Schranke . -
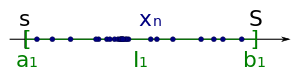 Als erstes Intervall der Intervallschachtelung wählt man .
Als erstes Intervall der Intervallschachtelung wählt man . -
 Das Intervall wird in zwei gleich große Teilintervalle unterteilt.
Das Intervall wird in zwei gleich große Teilintervalle unterteilt. -
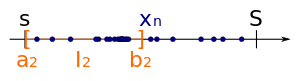 Als zweites Intervall der Intervallschachtelung wählt man das Teilintervall, welches unendlich viele Folgenglieder von besitzt. Wenn beide Teilintervalle unendlich viele Glieder von besitzen, wählt man irgendeines der beiden Teilintervalle als .
Als zweites Intervall der Intervallschachtelung wählt man das Teilintervall, welches unendlich viele Folgenglieder von besitzt. Wenn beide Teilintervalle unendlich viele Glieder von besitzen, wählt man irgendeines der beiden Teilintervalle als . -
 Das Intervall wird wieder in zwei Teilintervalle zerlegt.
Das Intervall wird wieder in zwei Teilintervalle zerlegt. -
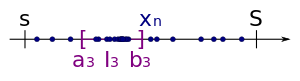 Auch hier wählt man das Teilintervall als drittes Intervall , welches unendlich viele Folgeglieder von besitzt.
Auch hier wählt man das Teilintervall als drittes Intervall , welches unendlich viele Folgeglieder von besitzt. -
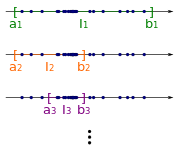 Diesen Prozess wiederholt man unendlich oft. So erhält man eine Intervallschachtelung . Aus dem Intervallschachtelungsprinzip folgt, dass es eine Zahl gibt, die in allen Intervallen enthalten ist. Diese Zahl ist dann auch Häufungspunkt der Folge .
Diesen Prozess wiederholt man unendlich oft. So erhält man eine Intervallschachtelung . Aus dem Intervallschachtelungsprinzip folgt, dass es eine Zahl gibt, die in allen Intervallen enthalten ist. Diese Zahl ist dann auch Häufungspunkt der Folge .
Verallgemeinerungen
Endlichdimensionale Vektorräume
Die komplexen Zahlen werden im Kontext dieses Satzes als zweidimensionaler reeller Vektorraum betrachtet. Für eine Folge von Spaltenvektoren mit n reellen Komponenten wählt man zuerst eine Teilfolge, die in der ersten Komponente konvergiert. Von dieser wählt man wieder eine Teilfolge, die auch in der zweiten Komponente konvergiert. Die Konvergenz in der ersten Komponente bleibt erhalten, da Teilfolgen konvergenter Folgen wieder konvergent mit demselben Grenzwert sind. Und so weiter, bis die n-te Teilfolge auch in der letzten Komponente konvergiert.
Unendlichdimensionale Vektorräume
Der Satz von Bolzano-Weierstraß gilt nicht in unendlichdimensionalen normierten Vektorräumen. So ist z. B. die Folge der Einheitsvektoren (0,0,...,0,1,0,...,0,...) im Folgenraum beschränkt, hat aber keinen Häufungspunkt, da alle Folgenglieder einen Abstand von voneinander haben. Dieses Gegenbeispiel lässt sich auf beliebige unendlichdimensionale normierte Räume verallgemeinern, man kann darin immer eine unendliche Folge von Vektoren der Länge 1 konstruieren, die untereinander paarweise einen Abstand von wenigstens 1/2 besitzen.
Als Ersatz für den Satz von Bolzano-Weierstraß in unendlichdimensionalen Vektorräumen existiert in reflexiven Räumen folgende Aussage, die aus dem Satz von Eberlein–Šmulian folgt: Jede beschränkte Folge eines reflexiven Raumes besitzt eine schwach konvergente Teilfolge. Zusammen mit den sobolevschen Einbettungssätzen liefert die Existenz von schwach konvergenten Teilfolgen beschränkter Folgen häufig Lösungen von Variationsproblemen und damit partiellen Differentialgleichungen.
Folgerungen und Verallgemeinerungen
Aus dem Satz von Bolzano-Weierstraß folgt, dass jede monotone und beschränkte Folge reeller Zahlen konvergiert (Monotoniekriterium) und dass eine stetige Funktion auf einem abgeschlossenen und beschränkten Intervall ein Maximum bzw. ein Minimum annimmt (Satz vom Minimum und Maximum).
Der Satz von Bolzano-Weierstraß ist eng verwandt mit dem Satz von Heine-Borel. Eine Verallgemeinerung beider Sätze auf topologische Räume ist folgender: Ein topologischer Raum ist genau dann ein kompakter Raum, wenn jedes Netz ein konvergentes Teilnetz hat.
Literatur
- Konrad Königsberger: Analysis 1. Springer, Berlin 2004, ISBN 3-540-41282-4
- Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8
![{\displaystyle (I_{k}=[u_{k},v_{k}])_{k\in \mathbb {N} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d032974b6c2b5eeaa5bb6e04e40e8a3579bf91)



![{\displaystyle I_{1}=[u_{1},v_{1}]=[-L,\,L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eedc0bc205b4ab8ae350661a5e84bae73e54305)

![{\displaystyle I_{k}=[u_{k},v_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4b652920a1c6053563bd436b8fb45153dd682a4)
![{\displaystyle [u_{k},t_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ff835c84d41e8560dd065cc07d126884c5bb75)
![{\displaystyle [t_{k},v_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7b84c9a615b409ae43f1813447d4947eb327c9)












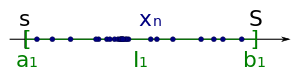
![{\displaystyle I_{1}=[s,S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58be63fbf6d3dff28ca6747569a558d5af61740e)