Elipsoid

Tento článek není dostatečně ozdrojován, a může tedy obsahovat informace, které je třeba ověřit.

Jste-li s popisovaným předmětem seznámeni, pomozte doložit uvedená tvrzení doplněním referencí na věrohodné zdroje.

Elipsoid je omezená kvadratická plocha. Někdy se chápe jako prostorové těleso tvořené množinou všech bodů, jejichž poloha vůči zadanému bodu (středu) splňuje podmínky dané následující nerovnicí. Pokud bychom znak ≤ nahradili znakem =, rovnici by splňovaly právě body na povrchu elipsoidu.

${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}\leq 1}$

kde a, b a c jsou konstantní kladná reálná čísla, určující délky poloos ve směru jednotlivých os. Uvedená definice předpokládá, že střed elipsoidu leží v počátku soustavy souřadnic a že osy elipsoidu jsou totožné s osami soustavy souřadnic. Pokud tomu tak není, je třeba nerovnici rozšířit o popis posunutí a otočení elipsoidu v prostoru.

Rovinnými řezy elipsoidu podél jednotlivých souřadnicových os jsou elipsy. Poloosy jednotlivých elips odpovídají poloosám elipsoidu.

Klasifikace elipsoidů

Elipsoid, jehož dvě poloosy jsou shodné, se nazývá rotační elipsoid nebo také sferoid. Rotační elipsoid lze také chápat jako těleso vzniklé rotací elipsy kolem jedné z jejich os. Při rotaci kolem hlavní osy se jedná o rotační elipsoid protáhlý, při rotaci elipsy kolem vedlejší osy jde o zploštělý rotační elipsoid.

Elipsoid, který má shodné všechny tři poloosy, je koule.

Budeme-li předpokládat, že a ≥ b ≥ c, potom:

• jestliže a > b > c, jde o obecný (trojosý) elipsoid
• jestliže a > b = c, jde o protáhlý (doutníkovitý) sferoid
• jestliže a = b > c, jde o zploštělý (diskovitý) sferoid
• jestliže a = b = c, jde o kouli

• 
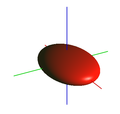  Trojosý elipsoid s poměrem poloos 3:2:1.
• 
  Protáhlý rotační elipsoid.
• 
  Zploštělý rotační elipsoid.

Vlastnosti

Elipsoid je jediná omezená kvadrika. Rovinným řezem je elipsa, jednobodová nebo prázdná množina.

V projektivní geometrii je ekvivalentní eliptickému paraboloidu a dvojdílnému hyperboloidu.

Objem libovolného elipsoidu je roven

${\displaystyle {\frac {4}{3}}\pi abc\,\!}$,

kde a, b, c jsou délky poloos.

Speciální případy

Objem protáhlého rotačního elipsoidu je

${\displaystyle V={\frac {4}{3}}\pi ab^{2}}$,

kde ${\displaystyle a>b}$.

Objem zploštělého rotačního elipsoidu je

${\displaystyle V={\frac {4}{3}}\pi a^{2}b}$,

kde ${\displaystyle a>b}$.

Povrch elipsoidu se počítá podstatně složitěji. S použitím číselné výstřednosti elipsy ${\displaystyle \varepsilon ={\frac {\sqrt {a^{2}-b^{2}}}{a}}}$ lze povrch protáhlého rotačního elipsoidu zapsat ve tvaru

${\displaystyle P=2\pi \left(b^{2}+ab{\frac {\operatorname {arcsin} \varepsilon }{\varepsilon }}\right)}$

Pro zploštělý elipsoid pak dostaneme výraz

${\displaystyle P=2\pi \left(a^{2}+{b^{2}}{\frac {\operatorname {artanh} \varepsilon }{\varepsilon }}\right)=2\pi \left(a^{2}+{\frac {b^{2}}{2\varepsilon }}\ln {\frac {1+\varepsilon }{1-\varepsilon }}\right)}$

Povrch trojosého elipsoidu se počítá složitěji pomocí eliptických integrálů.

Zobecněný hyperelipsoid

Typicky pracujeme s elipsoidem v trojrozměrném prostoru. Uvedenou definici lze zobecnit pro n-rozměrný prostor následovně (i nadále platí, že osy elipsoidu jsou totožné s osami soustavy souřadnic):

${\displaystyle \sum _{i=1}^{n}{x_{i}^{2} \over r_{i}^{2}}\leq 1}$

kde ${\displaystyle r_{i}}$ je vektor poloos v jednotlivých rozměrech. Pro ${\displaystyle n>3}$ jde o abstraktní matematické těleso, které je obtížné vizualizovat. Pro ${\displaystyle n=2}$ jde o elipsu v rovině. Pro ${\displaystyle n=1}$ jde o úsečku na přímce.

Referenční elipsoid

Polární souřadnice

Tato část článku potřebuje úpravy.

Můžete Wikipedii pomoci tím, že ji vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl, Encyklopedický styl a Odkazy.

Klasické kartézské souřadnice neposkytují dostatečně intuitivní představu o poloze bodu na povrchu elipsoidu. Pokud víme, že se pohybujeme po povrchu, stačí nám totiž pouhé dvě souřadnice místo tří. Při využití elipsoidu jako referenčního tělesa pro povrch planety se proto obvykle používají polární (úhlové) souřadnice: zeměpisná šířka a zeměpisná délka. V mnoha případech nám totiž stačí pracovat s body na povrchu referenčního elipsoidu a odchylky způsobené nadmořskou výškou nebo lokální odchylkou gravitačního potenciálu zanedbáváme. Pokud bychom je nechtěli zanedbávat, museli bychom soustavu polárních souřadnic doplnit o třetí rozměr, výšku.

• Délka bodu ${\displaystyle A}$ je úhel mezi rovinou ${\displaystyle xz}$ (tj. rovinou obsahující osy ${\displaystyle x}$ a ${\displaystyle z}$) a rovinou obsahující osu ${\displaystyle z}$ a bod ${\displaystyle A}$. Označme tuto rovinu ${\displaystyle \delta }$. Vzhledem k tomu, že délka může být kladná i záporná, známe nejen úhel, ale i směr rotace od výchozí roviny (úhel je orientovaný) a máme navíc informaci o polorovině, na které se daný bod nachází (rovina ${\displaystyle \delta }$ je rozdělena na poloroviny osou ${\displaystyle z}$). Na referenčním elipsoidu Země se délka určuje v rozsahu -180° až +180° (zápornou délku mají body, které mají zápornou kartézskou souřadnici ${\displaystyle y}$); u jiných těles se obvykle používá rozsah 0° až 360°.
• Šířka je úhel mezi rovinou ${\displaystyle xy}$ a přímkou ${\displaystyle r}$, která je podmnožinou roviny ${\displaystyle \delta }$ a prochází středem elipsoidu i bodem ${\displaystyle A}$. Šířka se určuje v rozsahu -90° až +90° (zápornou šířku mají body, které mají zápornou kartézskou souřadnici ${\displaystyle z}$).
• Výška je (případná) vzdálenost bodu ${\displaystyle A}$ od povrchu elipsoidu a jde o reálné číslo, které je zdola omezeno hodnotou ${\displaystyle -a}$ (opačné číslo k největší z poloos elipsoidu), shora omezené není. Jde-li o referenční elipsoid planety, udává se výška obvykle v metrech, popř. ve stopách.
• Šířka geodetická je úhel mezi rovinou ${\displaystyle xy}$ (tj. rovinou rovníku) a přímkou ${\displaystyle h}$. Přímka ${\displaystyle h}$ je normálou k tečné rovině elipsoidu v daném bodě a obecně nemusí procházet středem elipsoidu. Pro počty s geodetickou šířkou musí platit poněkud jiné definice, než jaké jsou použity v následujících příkladech. Proto pozor, o kterou šířku se jedná. Viz např. standard WGS 84.

Převod polárních souřadnic na kartézské

Poznámka: Při nasazení níže uvedeného postupu v praxi je třeba si ověřit, zda software, s jehož pomocí počítáme funkci tangens, očekává úhel ve stupních, nebo v radiánech. Stupně lze přepočítat na radiány vzorcem ${\displaystyle radi{\acute {a}}ny=stupn{\check {e}}{\pi \over 180}}$.

Poznámka: Použití funkce tg nelze doporučit, v blízkosti singularity vede k chybám. Místo toho lze vystačit s funkcemi sin, cos a návod by bylo vhodné upravit.

1. Mějme bod ${\displaystyle A}$ daný délkou ${\displaystyle \lambda }$, šířkou ${\displaystyle \phi }$ a výškou ${\displaystyle v}$.
2. ${\displaystyle y=x{\mbox{tg }}\lambda \,\!}$. Zvláštním případem je ${\displaystyle \|\lambda \|=90}$, kdy tangens není definován. Tehdy platí ${\displaystyle x=0\,\!}$.
3. ${\displaystyle z=({\sqrt {x^{2}+y^{2}}}){\mbox{tg }}\phi }$, kde ${\displaystyle {\sqrt {x^{2}+y^{2}}}}$ je poloměr ${\displaystyle \phi }$-té rovnoběžky. Zvláštním případem je ${\displaystyle \|\phi \|=90}$, kdy tangens není definován. Tehdy platí ${\displaystyle x=y=0\,\!}$.
4. Nyní již můžeme popsat polopřímku ${\displaystyle r}$, která vychází ze středu elipsoidu a prochází bodem ${\displaystyle A}$. Výše uvedené vztahy mezi ${\displaystyle x}$, ${\displaystyle y}$ a ${\displaystyle z}$ vycházejí z úhlů definujících polopřímku a platí proto pro každý její bod. Na polopřímce tedy leží i bod ${\displaystyle A_{1}=[1;{\mbox{tg }}\lambda ;({\sqrt {1+({\mbox{tg }}\lambda )^{2}}}){\mbox{tg }}\phi ]}$.
5. Potřebujeme zjistit, v jaké vzdálenosti od středu elipsoidu leží bod, ve kterém polopřímka ${\displaystyle r}$ protíná jeho povrch. Nejdříve tedy musíme zjistit souřadnice tohoto průsečíku. Hledáme takový skalár ${\displaystyle k_{Z}}$, že bod ${\displaystyle A_{Z}=k_{Z}\cdot A_{1}}$ leží na povrchu elipsoidu, tj. splňuje rovnici ${\displaystyle {{X_{Z}^{2}+y_{Z}^{2}} \over {a^{2}}}+{{Z_{Z}^{2}} \over {b^{2}}}=1}$.
6. Dosazením do této rovnice získáme ${\displaystyle k_{Z}={\sqrt {{A^{2}b^{2}} \over {b^{2}x_{1}^{2}+b^{2}y_{1}^{2}+a^{2}z_{1}^{2}}}}}$.
7. Vzdálenost bodu ${\displaystyle A_{Z}}$ od středu elipsoidu ${\displaystyle \|A_{Z}\|={\sqrt {x_{Z}^{2}+y_{Z}^{2}+z_{Z}^{2}}}}$.
8. Nyní hledáme takové ${\displaystyle k}$, že pro bod ${\displaystyle A}$, jehož souřadnice hledáme, platí ${\displaystyle A=k\cdot A_{1}}$. ${\displaystyle k}$ a ${\displaystyle k_{Z}}$ jsou ve stejném poměru, v jakém jsou vzdálenosti ${\displaystyle A}$ a ${\displaystyle A_{Z}}$ od středu, tedy ${\displaystyle k=k_{Z}{{\|A_{Z}\|+v} \over {\|A_{Z}\|}}}$. Souřadnice bodu ${\displaystyle A}$ pak už triviálně získáme pomocí ${\displaystyle k}$ a souřadnic ${\displaystyle A_{1}}$.

Příklad

Mějme bod určený polárními souřadnicemi

• ${\displaystyle \phi }$ = 50° s. š. = +50° = 0.872664626 radiánů
• ${\displaystyle \lambda }$ = 14° 30' v. d. = +14,5° = 0.253072741 radiánů
• ${\displaystyle v}$ = 250 m

Předpokládejme, že polární souřadnice jsou vztaženy k povrchu referenčního elipsoidu WGS-84, tedy

• a = 6 378 137 m
• b = 6 356 752,3 m

Potom

• ${\displaystyle A_{1}=[1;0.258618;1.230963]}$
• ${\displaystyle k_{Z}=3961374}$
• ${\displaystyle A_{Z}=[3961374;1024481;4876303]}$
• ${\displaystyle \|A_{Z}\|=6365562}$
• ${\displaystyle {{\|A_{Z}\|+v} \over {\|A_{Z}\|}}=1.000039}$
• ${\displaystyle A=[3961529;1024521;4876495]}$

Tedy

• x = 3 961 529 m
• y = 1 024 521 m
• z = 4 876 495 m

Převod kartézských souřadnic na polární

Poznámka: Použití funkce arctg je chybné, mj. nerespektuje znaménko výsledku. Návod by bylo vhodné upravit, ale bude složitější. Inspirací může být implementace funkce atan2 systému Matlab.

Předpokládejme, že pracujeme se zploštělým sferoidem, např. s referenčním elipsoidem Země. Pro obecný elipsoid lze postup zobecnit.

1. Mějme bod ${\displaystyle A}$ a jeho kartézské souřadnice ${\displaystyle x}$, ${\displaystyle y}$ a ${\displaystyle z}$.
2. Polopřímku ${\displaystyle r}$, která vychází ze středu elipsoidu a prochází bodem ${\displaystyle A}$, lze parametricky vyjádřit jako ${\displaystyle [0;0;0]+k\cdot A}$, kde ${\displaystyle k>0}$.
3. Protože bod ${\displaystyle A}$ může mít nenulovou výšku a nemusí tedy ležet přímo na povrchu elipsoidu, potřebujeme najít bod ${\displaystyle A_{Z}}$, který leží na průniku polopřímky ${\displaystyle r}$ s povrchem elipsoidu.
4. Tento bod musí současně splňovat rovnici pro polopřímku i rovnici pro povrch elipsoidu ${\displaystyle {{X_{Z}^{2}+y_{Z}^{2}} \over {a^{2}}}+{{Z_{Z}^{2}} \over {b^{2}}}=1}$.
5. Vyjádříme-li souřadnice ${\displaystyle A_{Z}}$ pomocí ${\displaystyle k_{Z}}$ a souřadnic ${\displaystyle A}$, dostaneme ${\displaystyle {{K_{Z}^{2}x^{2}+k_{Z}^{2}y^{2}} \over {a^{2}}}+{{K_{Z}^{2}z^{2}} \over {b^{2}}}=1}$.
6. ${\displaystyle {k_{Z}^{2}}={{A^{2}b^{2}} \over {b^{2}x^{2}+b^{2}y^{2}+a^{2}z^{2}}}}$
7. ${\displaystyle k_{Z}=\pm {\sqrt {{A^{2}b^{2}} \over {b^{2}x^{2}+b^{2}y^{2}+a^{2}z^{2}}}}}$
8. Dostaneme 2 koeficienty, jeden kladný a jeden záporný, protože přímka protne povrch elipsoidu na dvou místech. Jak už ale bylo zmíněno, zajímá nás pouze polopřímka vedoucí ze středu elipsoidu směrem k bodu ${\displaystyle A}$, využijeme tedy pouze kladný z obou koeficientů.
9. S pomocí koeficientu ${\displaystyle k}$ dostaneme souřadnice bodu ${\displaystyle A_{Z}=k_{Z}\cdot [x;y;z]}$.
10. Délka vektoru z bodu ${\displaystyle A_{Z}}$ do bodu ${\displaystyle A}$ odpovídá hledané nadmořské výšce: ${\displaystyle v=\pm {\sqrt {(x-x_{Z})^{2}+(y-y_{Z})^{2}+(z-z_{Z})^{2}}}}$. Směr vektoru nám prozradí, zda má být výška kladná, nebo záporná. Totéž lze vyčíst i z koeficientu ${\displaystyle k}$ - pokud je větší než 1, leží bod ${\displaystyle A_{Z}}$ na polopřímce ${\displaystyle r}$ až za bodem ${\displaystyle A}$, a výška bodu ${\displaystyle A}$ je tedy záporná. V opačném případě je výška kladná.
11. Délka ${\displaystyle \lambda ={\mbox{tg}}^{-1}{y \over {x}}}$
12. Šířka ${\displaystyle \phi ={\mbox{tg }}^{-1}{z \over {\sqrt {x^{2}+y^{2}}}}}$

Příklad

Mějme bod ${\displaystyle A}$ určený kartézskými souřadnicemi

• x = 1 113 547 m
• y = -4 823 300 m
• z = 4 008 571 m

Hledáme polární souřadnice tohoto bodu vztažené k povrchu referenčního elipsoidu WGS-84, tedy

• a = 6 378 137 m
• b = 6 356 752,3 m

Potom

• ${\displaystyle \phi =39}$
• ${\displaystyle \lambda =-77}$
• ${\displaystyle k_{Z}=0,999994}$
• ${\displaystyle A_{Z}=[1113540;-4823270;4008546]}$
• ${\displaystyle \|A_{Z}\|=6365562}$
• ${\displaystyle A-A_{Z}=[6,992792;-30,2891;25,17282]}$
• ${\displaystyle \|A-A_{Z}\|=40}$

Tedy

• φ = 39° s. š.
• λ = 77° z. d.
• v = 40 m

(Pohledem na mapu pak zjistíme, že tento bod leží na předměstí Washingtonu.)

Vzdálenost dvou bodů na povrchu elipsoidu

Tato část článku potřebuje úpravy.

Můžete Wikipedii pomoci tím, že ji vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl, Encyklopedický styl a Odkazy.

Vzdálenost dvou bodů na povrchu (nebo v blízkosti povrchu) elipsoidu nás zajímá zejména u referenčního elipsoidu, chceme-li určit vzdálenost dvou bodů na povrchu Země či jiné planety.

Po přímce

Nejkratší vzdáleností dvou bodů v prostoru je délka úsečky, kterou tyto body vymezují, tedy vzdálenost měřená na přímce. Pro praktické užití na referenčním elipsoidu má ovšem takto zjištěná vzdálenost zásadní nevýhodu, totiž že spojnice obou bodů typicky prochází pod povrchem elipsoidu a neodpovídá tedy vzdálenosti, kterou musí při přesunu mezi oběma body urazit např. letadlo. Pouze u malých vzdáleností je tento rozdíl zanedbatelný.

Vzdálenost bodů ${\displaystyle A}$ a ${\displaystyle B}$ lze přímo vypočítat z jejich kartézských souřadnic, stačí tedy převést polární souřadnice na kartézské podle výše uvedeného postupu.

${\displaystyle d={\sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}}}$

Příklad

Mějme body A (Praha) a B (Washington) jako ve výše uvedených příkladech, tedy

• A = [3961529; 1024521; 4876495]
• B = [1113547; -4823300; 4008571]

Potom

• (B-A) = [-2847982,876; -5847821,155; -867924,0585]
• d = 6 562 112 m

Po elipse

Vzdálenost vedená po povrchu elipsoidu by byla délka úseku elipsy, která prochází oběma body a má střed shodný se středem elipsoidu. Tato elipsa je průnikem povrchu elipsoidu a roviny definované středem elipsoidu a oběma body, jejichž vzájemnou vzdálenost měříme. Problém je, že neznáme poloosy této elipsy; víme pouze, že leží někde mezi největší a nejmenší poloosou elipsoidu. Můžeme však aspoň provést horní a dolní odhad vzdálenosti, pokud budeme místo elipsy postupně uvažovat kružnice s poloměry odpovídajícími největší a nejmenší poloose elipsoidu. Tento postup navíc nezohledňuje případnou výšku bodů A a B nad povrchem elipsoidu.

Při cestování po dráze dané elipsou se středem uprostřed elipsoidu se soustavně mění azimut, tedy úhel mezi směrem pohybu a severem! Přesun z bodu A do bodu B lze také provést po loxodromě (anglicky rhumb line), tedy čáře protínající všechny poledníky pod stejným úhlem; taková trasa však bude delší než trasa po elipse. I tento rozdíl je pro blízké body zanedbatelný.

• Pro změření úseku kružnice mezi body ${\displaystyle A}$ a ${\displaystyle B}$ potřebujeme znát úhel ${\displaystyle \gamma }$ mezi přímkami ${\displaystyle a}$ a ${\displaystyle b}$, přičemž přímka ${\displaystyle a}$ prochází bodem ${\displaystyle A}$, přímka ${\displaystyle b}$ prochází bodem ${\displaystyle B}$ a obě procházejí středem kružnice.
• Velikost úhlu ${\displaystyle \gamma }$ dokážeme určit pomocí goniometrických funkcí, pokud budeme znát polohu bodu ${\displaystyle K}$, ve kterém přímka ${\displaystyle c}$, spojující body ${\displaystyle A}$ a ${\displaystyle B}$, protíná kolmici na ni vedenou ze středu elipsoidu ${\displaystyle S}$.
  • Přímku ${\displaystyle c}$ lze popsat jako ${\displaystyle C=A+k\cdot (B-A)}$, kde ${\displaystyle k}$ je reálné číslo a ${\displaystyle (B-A)}$ je vektor vedoucí z bodu ${\displaystyle A}$ do bodu ${\displaystyle B}$. Pro každý bod ${\displaystyle C}$ přímky ${\displaystyle c}$ existuje skalár ${\displaystyle k}$ takový, že uvedená rovnice platí. Náš bod ${\displaystyle K}$ má ležet na přímce ${\displaystyle c}$, budeme tedy hledat jemu odpovídající ${\displaystyle k}$.
  • Přímku ${\displaystyle v}$, která prochází body ${\displaystyle S}$ a ${\displaystyle K}$, lze popsat jako ${\displaystyle V=S+l\cdot (K-S)}$. Protože bod ${\displaystyle S}$ je střed elipsoidu a počátek soustavy souřadnic, platí ${\displaystyle S=[0;0;0]}$, a tedy ${\displaystyle V=l\cdot K}$.
  • Protože dále ${\displaystyle v}$ má být kolmá na ${\displaystyle c}$, musí platit, že skalární součin jejich směrových vektorů je roven nule. Naším směrovým vektorem pro přímku ${\displaystyle c}$ je ${\displaystyle (B-A)}$, pro přímku ${\displaystyle v}$ je to (zatím neznámé) ${\displaystyle K}$, tedy ${\displaystyle x_{(B-A)}x_{K}+y_{(B-A)}y_{K}+z_{(B-A)}z_{K}=0\,\!}$.
  • Dosadíme-li do právě uvedené rovnice vyjádření bodu ${\displaystyle K}$ jako prvku přímky ${\displaystyle c}$, dostaneme rovnici o jedné neznámé ${\displaystyle k}$: ${\displaystyle x_{(B-A)}(x_{A}+kx_{(B-A)})+y_{(B-A)}(y_{A}+ky_{(B-A)})+z_{(B-A)}(z_{A}+kz_{(B-A)})=0\,\!}$.
  • Úpravou rovnice dostaneme ${\displaystyle k=-{{X_{A}(x_{B}-x_{A})+y_{A}(y_{B}-y_{A})+z_{A}(z_{B}-z_{A})} \over {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}}}$.
  • Získané ${\displaystyle k}$ dosadíme do rovnice ${\displaystyle K=A+k\cdot (B-A)}$ a dostaneme souřadnice bodu ${\displaystyle K}$.
• Změříme úsečky AK, KB a KS. Např. ${\displaystyle \|AK\|={\sqrt {(x_{K}-x_{A})^{2}+(y_{K}-y_{A})^{2}+(z_{K}-z_{A})^{2}}}}$.
• Vypočítáme úhel ${\displaystyle \gamma ={\mbox{tg}}^{-1}{{\|AK\|} \over {\|KS\|}}+{\mbox{tg}}^{-1}{{\|KB\|} \over {\|KS\|}}}$.
• Jestliže jsme úhel ${\displaystyle \gamma }$ dostali ve stupních, převedeme ho na radiány: ${\displaystyle radi{\acute {a}}ny=stupn{\check {e}}{\pi \over 180}}$.
• Délku úseku kružnice vypočítáme jako ${\displaystyle d=\gamma r\,\!}$, kde ${\displaystyle r}$ je poloměr kružnice.

Příklad

Mějme body A (Praha) a B (Washington) jako ve výše uvedených příkladech, tedy

• A = [3961529; 1024521; 4876495]
• B = [1113547; -4823300; 4008571]

a poloosy referenčního elipsoidu

• a = 6 378 137 m
• b = 6 356 752,3 m

Potom

• (B-A) = [-2847982,876; -5847821,155; -867924,0585]
• k = 0,499427705
• K = [2539167,869; -1896042,727; 4443029,462]
• |AK| = 3 277 300,419 m
• |KB| = 3 284 811,352 m
• |SK| = 5 457 367,707 m
• γ = 1,082625728 rad = 62,03°

Pro kružnice s maximálním (a) a minimálním (b) poloměrem pak získáme horní a dolní odhad vzdálenosti po elipse:

• da = 6 905 135 m
• db = 6 881 984 m

Jak vidíme, chyba způsobená tím, že se pohybujeme po kružnici místo po elipse, je relativně malá (23 km), zatímco rozdíl mezi vzdáleností po kružnici a vzdáleností po přímce je poměrně značný (320, resp. 343 km).

Odkazy

Související články

• Sféroid
• Geoid
• Geometrický útvar
• Kvadrika (kvadratická plocha)
• Koule
• Elipsa

Externí odkazy

• Obrázky, zvuky či videa k tématu elipsoid na Wikimedia Commons